CA——M-PID

参考链接：
- 原始论文：Bid Optimization by Multivariable Control in Display Advertising, KDD 2019, Alibaba

整体思路介绍

实时竞价（RTB）是展示广告中的重要范式，广告主利用需求方平台（DSP）提供的信息和算法来提升广告效果
- DSP面临的一个常见问题是在预算约束下帮助广告主获取最大价值
- 实际场景中，广告主通常会添加某些关键绩效指标（KPI）约束，广告 campaign 必须满足这些约束
论文研究广告主旨在最大化转化量并将每次点击成本（CPC）作为KPI约束的常见情况
- 论文将此问题转化为线性规划问题，并利用 primal-dual 方法推导出最优竞价策略
- 为了解决适用性问题，论文提出了一种基于反馈控制的解决方案，并设计了多变量控制系统
基于淘宝网真实数据的实证研究验证了论文的方法相比行业最新实践的有效性和优越性

一些讨论

在在线展示广告中，广告主为展示广告的机会支付一定费用。实时竞价（RTB）是展示广告中最流行的范式。RTB允许广告主在展示级别对广告机会进行竞价，出价最高的广告主赢得展示其广告的机会（每个广告机会的竞价价格可以跟随其效用和成本而改变，这使得广告主能够利用DSP提供的扩展信息和算法）
DSP面临的一个常见问题是在预算约束下帮助广告主获取尽可能多的价值。已有一些竞价策略和算法被提出，用于在预算约束下最大化广告价值。因此，广告主只需设置广告 campaign 的预算，DSP会代表广告主计算竞价价格
除了预算约束外，广告主通常会添加某些关键绩效指标（key performance indicator，KPI）约束，广告 campaign 必须满足这些约束
- KPI设置的必要性 ：广告主设置此类KPI约束是因为仅具有单一预算约束的广告 campaign 可能会受到竞价环境波动导致的流量巨大变化的影响。例如，某些日期的广告机会可能变得非常昂贵，以至于广告主无法承担所有预算
- 解决方案1 ：一种解决方案是不断调整每日预算以控制投资，这对广告主来说成本高昂甚至不切实际
- 解决方案2 ：另一种解决方案是设置某些KPI约束，每千次展示成本（CPM）和每次点击成本（CPC）约束，对广告投放的总成本有很强的影响
  - 通过设置此类KPI约束，广告主可以对总成本施加限制，并在广告机会不值得时避免花费所有预算，从而免去频繁调整广告 campaign 设置的繁重工作
  - 此外，KPI约束还作为实时代理来调节广告效果。在大多数情况下，广告主最终希望获得转化。然而，转化是稀疏且延迟的，这使得广告主无法实时评估广告效果。因此，广告主使用DSP提供的KPI来评估广告的预期价值 ，并将其设置为约束以确保广告效果可控
- 论文重点关注CPC约束 ，这是最常见的KPI约束之一。论文的方法可以推广到其他与成本相关的KPI约束 ，如CPM约束
论文提出了在预算和CPC约束下最大化广告转化量的最优竞价策略。在这项工作中，竞价优化被表述为一个线性规划问题，并利用 primal-dual 方法推导出最优竞价策略
论文提出了基于最优竞价策略的多变量控制系统 ，以解决适用性问题，特别是在工业应用中面临的动态环境
- PID控制系统 ：基于对竞价策略中超参数的分析，论文声称这些超参数在实现相应约束方面具有强大的控制能力，并设计了独立的PID控制系统
- 模型预测控制系统 ：考虑到耦合效应，论文通过提出模型预测控制系统进一步提高了系统的性能
论文所提出的系统已在真实工业数据集上实现和评估。基于淘宝网真实数据的实验表明，这些系统在实现约束方面具有强大的控制能力。论文还将论文的方法与行业最新实践进行了比较，结果显示了论文方法的优越性。论文工作的主要贡献可以总结如下：
- 论文提出了在预算和CPC约束下最大化转化量的最优竞价策略
- 论文设计了多变量控制系统 ，以应对在工业应用中应用竞价策略时的动态环境
- 进行了广泛的实验，结果证明了论文方法的优势

竞价策略

在本节中，论文首先回顾RTB生态系统的一些基础知识，然后提出竞价优化问题。接着，论文推导最优竞价策略，并讨论竞价策略的特性

RTB生态系统

RTB的工作流程如图1所示，每一步如下：
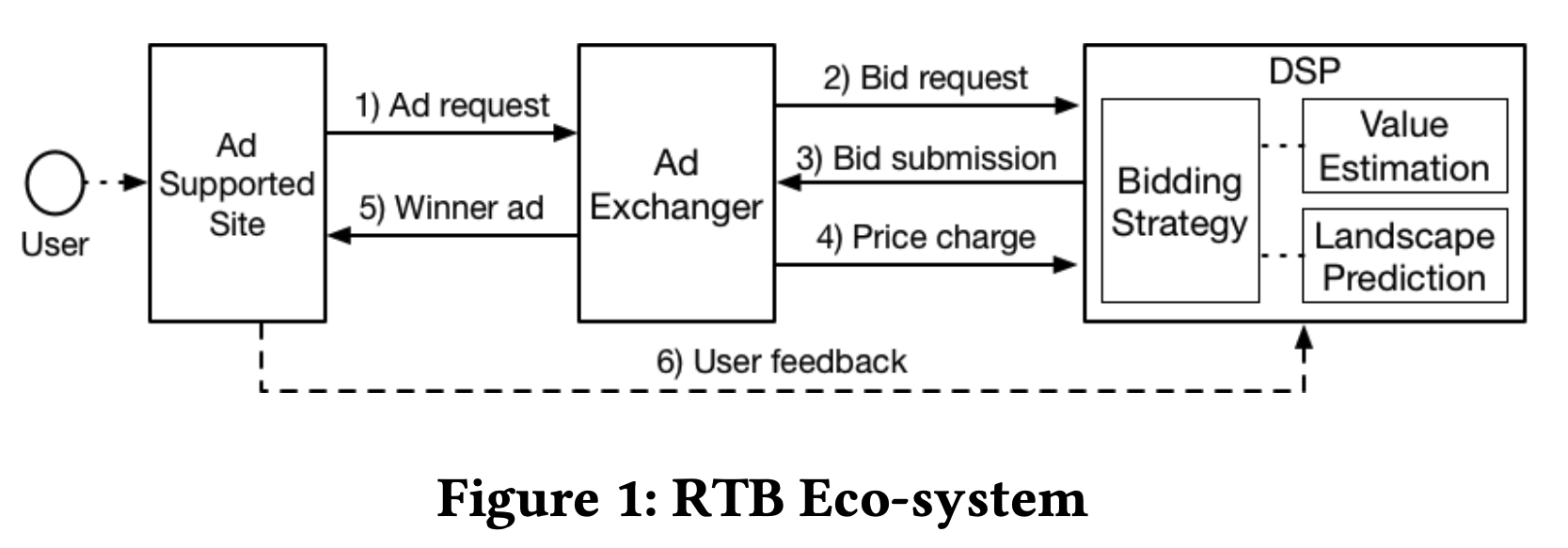
- 1）用户访问一个支持广告的网站，网站向广告交换平台发送广告请求
- 2）广告交换平台发起拍卖并向DSP请求竞价
- 3）DSP代表广告主向广告交换平台提交竞价价格和广告
- 4）广告交换平台进行拍卖并向获胜的DSP收取广告机会费用
- 5）获胜者的广告被发送到网站
- 6）用户的后续反馈会被发送回相应的DSP
当DSP从广告交换平台接收到竞价请求时，它会通过其竞价策略为广告主计算竞价价格。由于转化是大多数广告主的目标事件 ，几乎所有竞价策略（包括论文的策略）都严重依赖于学习模型的能力来估计广告点击率（CTR）和转化率（CVR）。此外，一些DSP还可能基于对获胜价格（竞价环境预测）的预测来制定竞价策略。论文假设估计和预测问题已经解决，点击和转化的预期概率可以分别通过CTR和CVR量化
当DSP在拍卖中赢得展示广告的机会时，它会被收取一个价格。在广义第二价格（GSP）拍卖机制下，该价格等于第二高的竞价价格，该机制在工业平台中被广泛采用。还有一些其他拍卖机制，如Vickrey-Clarke-Groves拍卖机制（VCG）。在论文中，不失一般性，论文基于最常见的GSP拍卖机制进行讨论和建模
用户对广告的任何反馈，如点击和转化，都会被发送回相应的DSP。DSP可以利用这些反馈来训练预测模型，并及时调整其竞价策略。此外，这些反馈会被DSP整合并暴露给广告主。在论文提出的系统中，论文利用这些反馈，并在广告 campaign 的生命周期中持续微调竞价策略

问题建模

假设一天中有 $N$ 个广告机会，论文按生成顺序将每个广告机会索引为 $opportunity_i$ 。每个广告机会对广告主具有不同的价值，论文用 $v_i = CTR_i \cdot CVR_i$ 表示 $opportunity_i$ 对广告主的价值。基于 $v_i$ ，计算竞价价格 $bid_i$ 并提交给广告交换平台。每个广告机会有一个获胜价格 $wp_i$ 。从广告主的角度来看， $wp_i$ 等于其他广告主的最高竞价价格。如果 $bid_i$ 高于 $wp_i$ ，这意味着广告主将赢得广告机会并在GSP拍卖机制下被收取 $wp_i$ ，论文将 $x_i$ 设为1，否则设为0。广告 campaign 的总价值和总成本如公式（1）和公式（2）所示
$$
Value = \sum_{i=1\ldots N} x_i \cdot v_i \\
Cost = \sum_{i=1\ldots N} x_i \cdot wp_i
$$
论文在公式（3）中定义CPC。值得注意的是，论文用CTR替换了实际点击，这为论文提供了更简洁的公式。这种替换在很大程度上促进了论文的理论分析，并且对后续的实际系统设计影响很小
$$CPC = \frac{\sum_{i=1\ldots N} x_i \cdot wp_i}{\sum_{i=1\ldots N} x_i \cdot CTR_i} \tag{3}$$
转化是广告主最终希望的结果。因此，论文通过 $CTR_i \cdot CVR_i$ 量化 $v_i$ 。请注意，必须考虑 $CTR_i$ ，因为只有在点击后才能生成转化，而CVR是以点击为条件的。论文将问题总结如下，并将其建模为（LP1，包含约束（4）和约束（5）），论文在预算 $B$ 下最大化广告转化量，并保证CPC不超过给定值 $C$ ：
$$
\begin{align}
\max_{x_i} \sum_{i=1\ldots N} x_i \cdot CTR_i \cdot &CVR_i \text{(LP1)}\\
\text{s.t.} \quad \quad \sum_{i=1\ldots N} x_i \cdot wp_i &\leq B \\
\frac{\sum_{i=1\ldots N} x_i \cdot wp_i}{\sum_{i=1\ldots N} x_i \cdot CTR_i} &\leq C \\
0 \leq x_i &\leq 1, \forall i
\end{align}
$$

最优竞价策略

问题（LP1）实际上是一个线性规划问题，即在线性约束下找到最优的 $x_i$ 以最大化目标函数。已有许多算法直接解决此类问题，但论文的目标是推导最优竞价策略而非分配策略。换句话说，论文本质上并不关心 $x_i$ 的值，而是关心内在影响 $x_i$ 的竞价策略。基于此考虑，论文创造性地采用 primal-dual 方法。每个线性规划问题（称为原始问题）都可以转换为对偶问题。此外，根据对偶定理（duality theorem），最优原始解可以通过相应的对偶解获得。这些数学特性为论文提供了一些启示，论文整合原始空间和对偶空间，推导出以下定理：
定理2.1 ：最优竞价策略的公式为：
$$bid_i = \frac{1}{p + q} \cdot CTR_i \cdot CVR_i + \frac{q}{p + q} \cdot CTR_i \cdot C \tag{6}$$
- 最优竞价策略在公式（6）中给出，其中 $p$ 和 $q$ 是从对偶空间引入的超参数，对应于最优对偶解。论文将在后续章节中研究 $p$ 和 $q$ 的性质。现在，论文给出定理2.1的证明
证明：（LP1）被转换为对偶问题：
$$
\begin{align}
\min_{p, q, r_i} B \cdot p + \sum_{i=1\ldots N} r_i \quad &\text{(LP2)} \\
\text{s.t.} wp_i \cdot p + (wp_i - CTR_i \cdot C) q + r_i &\geq CTR_i \cdot CVR_i, \forall i \\
p &\geq 0,\\ q &\geq 0,\\ r_i &\geq 0, \forall i
\end{align}
$$
- 假设原始问题（LP1）的最优解为 $x_i^*, \forall i = 1, \ldots, n$ ，对应的对偶问题（LP2）的最优解为 $p^*, q^*, \{r_i^* | i = 1, \ldots, n\}$ 。根据互补松弛定理，论文得到：
  $$x_i^* \cdot (CTR_i \cdot CVR_i - wp_i \cdot p - (wp_i - CTR_i \cdot C) q - r_i) = 0, \forall i \\
  (x_i^* - 1) \cdot r_i^* = 0, \forall i \tag{8&9}$$
- 论文巧妙地设最优出价形式为：
  $$\color{red}{bid_i^* = \frac{1}{p^* + q^*} CTR_i \cdot CVR_i + \frac{q^*}{p^* + q^*} C \cdot CTR_i}$$
  - 特别说明 ：这里的公式形式是有规律的，直接对原始问题构造拉格朗日函数，然后令原始拉格朗日函数对 $x_i$ 的偏导数为0，即可得到 $wp_i$ 的形式，其他类似约束问题也可以这样求解最优出价形式
- 最优出价形式的验证 ：
  - 将公式（8）转换为公式（10）：
    $$x_i^* \cdot ((bid_i^* - wp_i)(p^* + q^*) - r_i^*) = 0, \forall i \tag{10}$$
  - 根据公式（10）：
    - 如果广告 campaign 赢得 $opportunity_i$ ，即 $\color{red}{x_i^* > 0}$ ，则 $(bid_i^* - wp_i)(p^* + q^*) - r_i^* = 0$ 。同时， $p^* \geq 0, q^* \geq 0, r_k \geq 0$ ，因此 $\color{red}{bid_i^* \geq wp_i}$
    - 如果广告 campaign 失去 $opportunity_i$ ，即 $\color{red}{x_i^* = 0}$ ，我们可以从公式（9）推导出 $r_i^* = 0$ 。因此，根据公式（7），论文得到 $(bid_i^* - wp_i)(p^* + q^*) < 0$ ，即 $\color{red}{bid_i^* \leq wp_i}$
综上所述，对于任何 $opportunity_i$ ，竞价策略将保证 $x_i$ 是最优的，从而得到（LP1）的最优解。也就是说，当最优 $x_i$ 为1（广告 campaign 应赢得 $opportunity_i$ ）时，基于最优竞价策略的竞价价格 $bid_i$ 高于 $wp_i$ ，这将保证广告 campaign 赢得 $opportunity_i$ 。当最优 $x_i$ 为0时，推理相同。因此，广告 campaign 只需按照公式（6）中的最优竞价策略进行竞价，总广告价值将在约束条件下最大化。
关于 $p$ 和 $q$ 的讨论 ：公式（6）并未明确给出 $p$ 和 $q$ 的值。实际上，通过使用成熟的线性规划算法求解对偶问题，可以轻松推导出最优的 $p$ 和 $q$ 。此类工作对论文的理解没有贡献，因此论文在此不讨论如何计算 $p$ 和 $q$ 的值
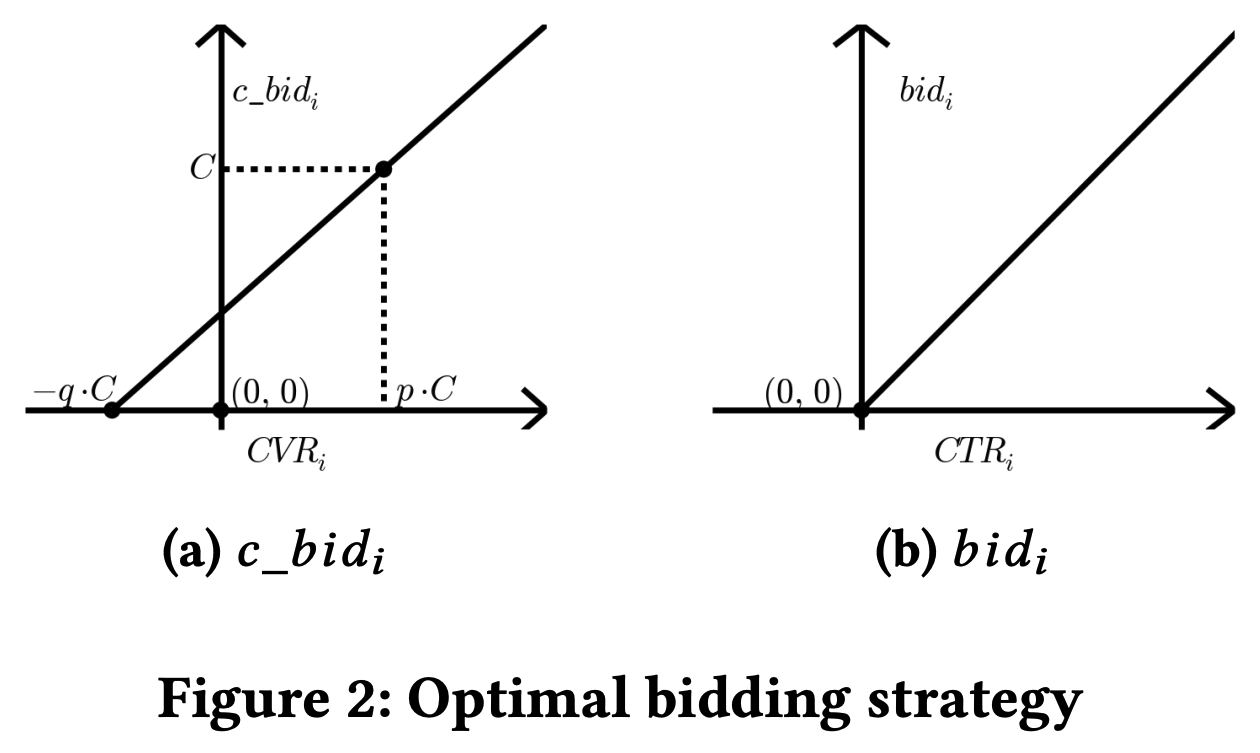
引入点击出价 $c\_bid_i$ 变量 ：论文将（LP1）的最优竞价策略重新表述为两个阶段，如公式（11）、公式（12）和图2所示，其中 $c\_bid_i$ 可以视为点击的竞价价格。当一个广告机会到来时，论文首先确定点击的竞价价格，即 $c\_bid_i$ 。在确定 $c\_bid_i$ 后，最终竞价价格通过将 $c\_bid_i$ 与 $CTR_i$ 相乘来计算，这一过程可以自动完成，并在后续讨论中省略
$$c\_bid_i = \frac{1}{p + q} \cdot CVR_i + \frac{q}{p + q} \cdot C \tag{11}$$
进一步地，有曝光出价为：
$$
\begin{align}
bid_i &= c\_bid_i \cdot CTR_i \\
&= \left( \frac{1}{p + q} \cdot CVR_i + \frac{q}{p + q} \cdot C \right) \cdot CTR_i \tag{12}
\end{align}
$$
此外，在GSP拍卖机制下，点击的成本自然不高于点击的竞价价格，因此 $c\_bid_i$ 直接与CPC相关。因此，为了便于演示，论文将讨论重点放在点击的竞价价格（ $c\_bid_i$ ）上，而非最终竞价价格
论文以一些明显的事实开始讨论最优竞价策略，如图2a所示
- 第一，点击的竞价价格与 $CVR_i$ 严格正相关。这很有道理：论文应该为更有价值的点击提供更高的竞价价格，为价值较低的点击提供较低的价格
- 第二，竞价价格相对于 $CVR_i$ 是线性的。这是一个自然的结果，因为论文要最大化价值的和，而价值是相对于 $CVR_i$ 本身的线性函数
- 第三，竞价策略肯定会穿过图中强调的两个点。论文将在后续分析中详细讨论这一点
- CVR为0时，点击出价不为0 ：论文中有一个不寻常的事实：与广泛采用的竞价策略不同，该函数不一定通过原点。具体来说，即使广告机会对广告主没有价值，竞价价格也可能非零。论文为一个没有价值的广告机会出非零价格有点反直觉
  - 论文陈述原因如下：考虑到给定CPC约束 ，竞价策略试图赢得一些廉价的广告机会，即使没有任何价值，以降低整体CPC ，从而赢得一些具有高CPC的有价值广告机会

系统设计

在本节中，论文解决了竞价策略在工业场景中的适用性问题，并提出了基于反馈控制的解决方案。基于对最优竞价策略中超参数的分析，论文提出了多变量控制系统

适用性问题

如（LP2）所示，为了求解线性规划问题并获得最优竞价策略，论文需要准确知道一天中每个广告机会的信息，包括获胜价格、CTR和CVR。然而，在现实世界中，这些信息直到一天结束时才能获得，而最优竞价策略需要在广告 campaign 开始前确定
除了在广告 campaign 开始前难以精确预测所有这些信息之外，如何预测一天中的广告机会本身仍然是一个开放性问题 ，因为动态环境（dynamic environment）
- 有人可能认为有许多统计算法可以解决此类问题：可以从足够的历史数据中推导出最优解，并应用于未来（此类算法的一个强假设是变量的分布是平稳的）。然而，在动态RTB环境中，不仅广告机会的分布 ，其他因素如获胜价格、CTR和CVR的分布也不是平稳的。因此，基于历史数据推导的最优竞价策略对未来不再最优 ，甚至可能打破CPC约束

基于反馈控制的解决方案

如上一节所述，由于动态竞价环境，论文基于历史数据推导的竞价策略可能不可靠。因此，论文需要利用实时信息来调整竞价策略。反馈控制通过从系统输出和外部噪声中处理动态系统(dynamic system)（Kumar等，2014），因其鲁棒性和有效性而在工业中被广泛采用。反馈控制系统(feedback control problem)通过基于系统输出的反馈调整系统输入来实现理想的性能
在论文的场景中，论文自然可以将竞价策略和RTB环境集成为一个动态系统 ，并将竞价策略的超参数 $p$ 和 $q$ 视为系统的输入。通过这样做，问题被转化为反馈控制问题
仍然有一个问题：什么是理想的性能，因此论文应该关心输出的哪些反馈？首先，论文的目标是最大化广告价值并控制CPC。其次，为了最大化广告价值，论文应该在时间上分散预算支出以赢得有价值的广告机会。因此，论文需要同时控制预算支出和CPC。论文提出以下反馈解决方案：为了提高广告性能，论文基于实时反馈控制预算支出和CPC
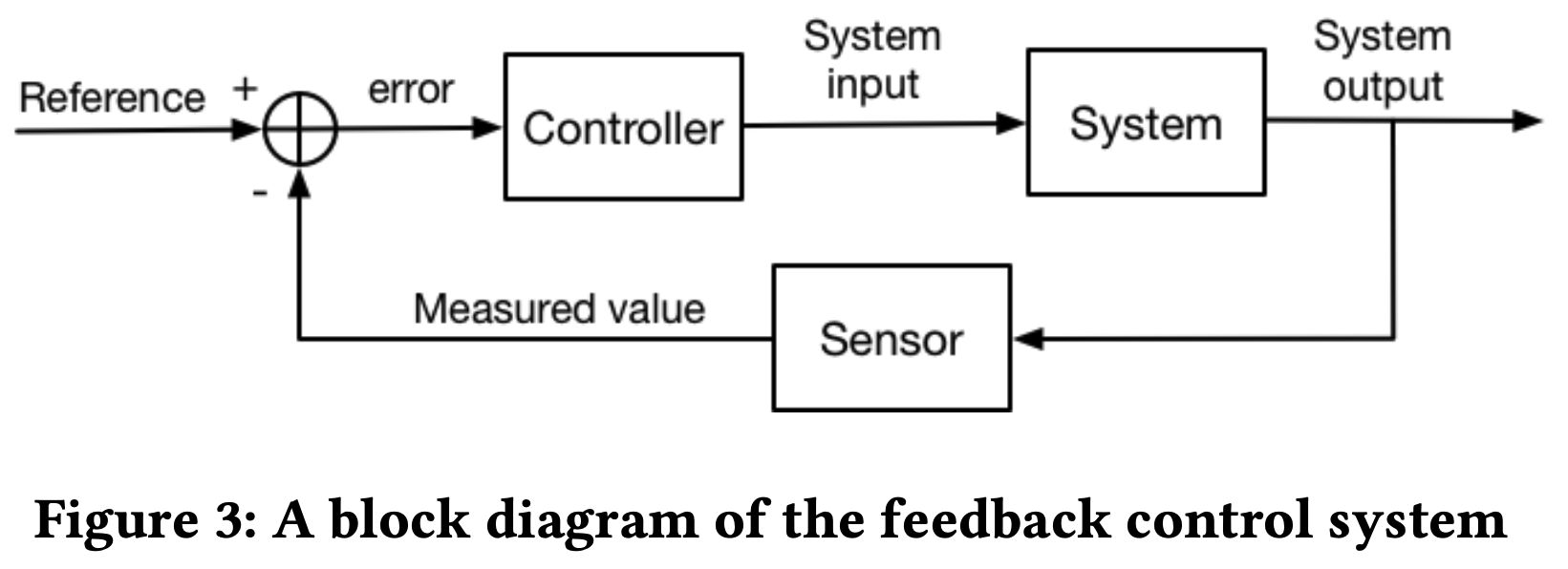
关于控制器的介绍 ：论文简要介绍标准的反馈控制系统。反馈控制系统的框图如图3所示。输出的期望值称为参考值 ，根据具体任务预先设定。传感器从系统输出中测量变量的实际值，并将其传输给控制器。通过比较测量值和参考值 ，控制器会根据其预定义的算法或策略调整系统输入，以减小它们之间的差异
- 比例-积分-微分（Proportional-Integral-Derivative，PID）控制器（Bennett，1993）是工业中最广泛采用的反馈控制器。已知PID控制器在缺乏对底层过程了解的情况下提供最佳性能（Åström和Hägglund，1995）
- PID控制器用法介绍 ：PID控制器在每个时间步 $t$ 连续计算测量值 $y(t)$ 和参考值 $r(t)$ 之间的误差 $e(t)$ ，并基于误差的比例、积分和微分项的组合产生控制信号 $u(t)$ 。控制信号 $u(t)$ 然后被发送以通过执行器模型 $\phi(x(0), u(t))$ 调整系统输入 $x(t)$ 。在在线广告场景中，使用离散时间步 $(t_1, t_2, \ldots)$ 是实际和常见的，因此PID的过程可以表示为以下公式，其中 $k_p$ 、 $k_i$ 和 $k_d$ 是PID控制器的权重参数

$$e(t) = r(t) - y(t) \tag{13}$$

$$u(t) = k_p e(t) + k_i \sum_{k=1\ldots t} e(k) + k_d (e(t) - e(t-1)) \tag{14}$$

$$x(t+1) = \phi(x(0), u(t)) \tag{15}$$

超参数分析

多变量下的控制方法 ：论文已经将问题转化为反馈控制问题，并在上一节中确定了动态系统（竞价策略和RTB）、输入参数（ $p$ 和 $q$ ）和输出变量（预算支出和CPC）。挑战在于如何通过调整 $p$ 和 $q$ 同时控制预算支出和CPC。由于多输入参数和多输出变量，论文不能直接在论文的场景中应用PID控制器（PID是单输入参数和单输出变量系统设计的）。已有一些多变量控制方法，如模型预测控制（Rawlings和Mayne，2009），用于处理此类系统，论文将在下一节的设计中利用其基本思想。在本节中，论文重新审视公式（11）中的最优竞价策略，并分享论文设计多变量控制系统的想法
回顾最优点击出价公式：
$$c\_bid_i = \frac{1}{p + q} \cdot CVR_i + \frac{q}{p + q} \cdot C \tag{11}$$
论文分析超参数 $p$ 和 $q$ 如何对公式（11）中的竞价策略做出贡献。请回顾 $p$ 和 $q$ 是由约束（4）和（5）引入的对偶变量，论文探讨它们与相应约束的关系
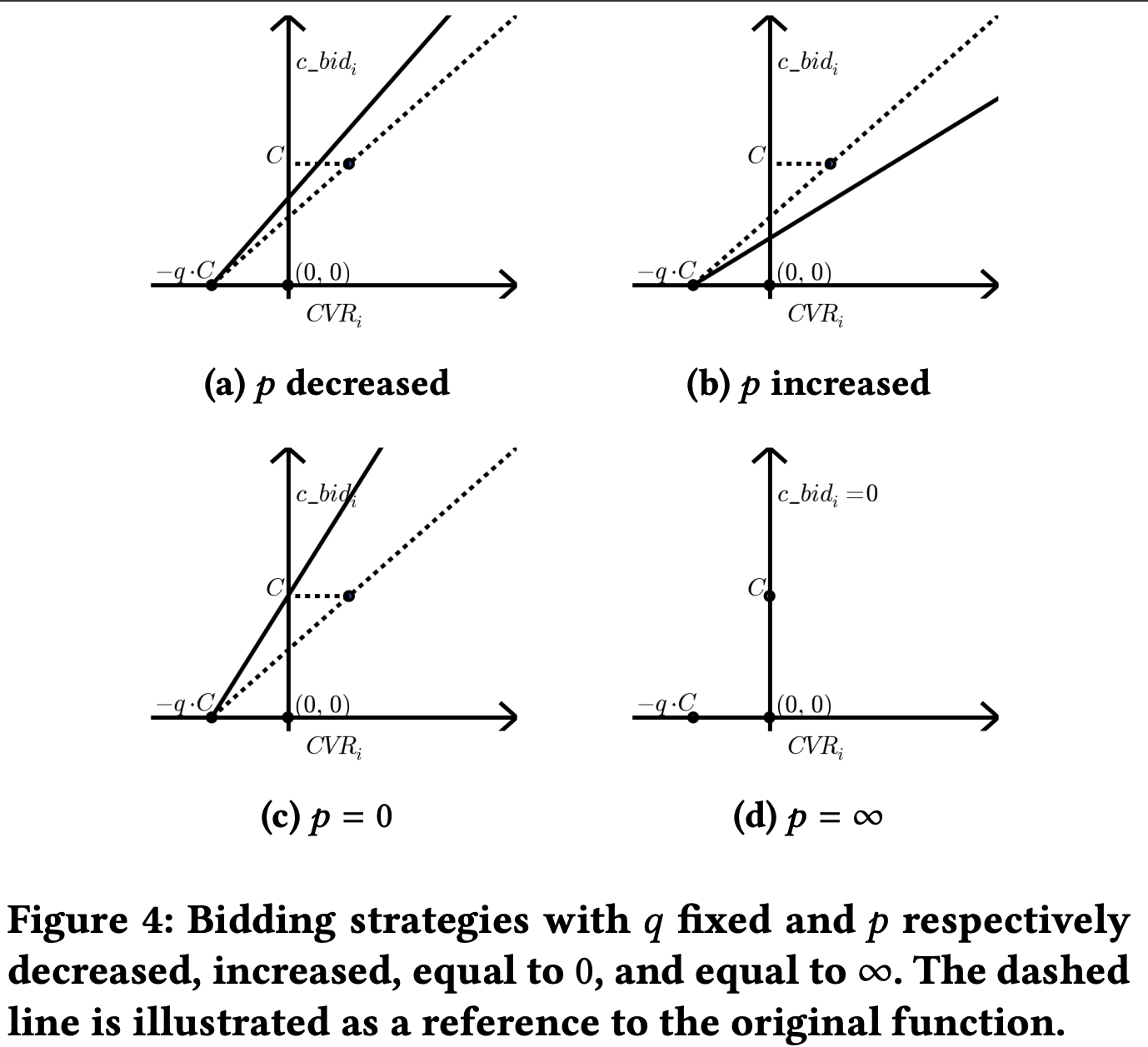
图4显示了在固定 $q$ 的情况下 ， $p$ 分别减小、增大、等于0和等于 $\infty$ 时的最优竞价策略。值得注意的是，竞价价格将直接影响预期成本：更高的竞价价格会导致更多成本，因为广告 campaign 可能赢得更多广告机会。如图4所示，随着 $p$ 的增加或减少，竞价价格通常会降低或提升
- 当论文增加 $p$ 时 ，竞价策略将围绕点 $(-q \cdot C, 0)$ 顺时针旋转。结果是：高于零的竞价价格将降低 ，低于零的竞价价格将提升（注：低于零的价格图上没有画出来，实际上，低于0时不会出价），从而预期成本将减少。以 $p = \infty$ 和 $p = 0$ 作为极端例子。当 $p = \infty$ 时，广告 campaign 的竞价价格始终为零，因此永远不会被收费。当 $p = 0$ 时，预算不再是一个约束。竞价价格不会无限高，因为仍然存在CPC约束，并且竞价策略的斜率完全由 $q$ 控制。如果论文同时将 $q$ 设为0，这意味着CPC约束也被移除，竞价价格将无限高，广告 campaign 将赢得所有广告机会。根据图示，论文声称 $p$ 对预算支出具有直接和有效的控制能力，并且可以明确降低预算支出速度
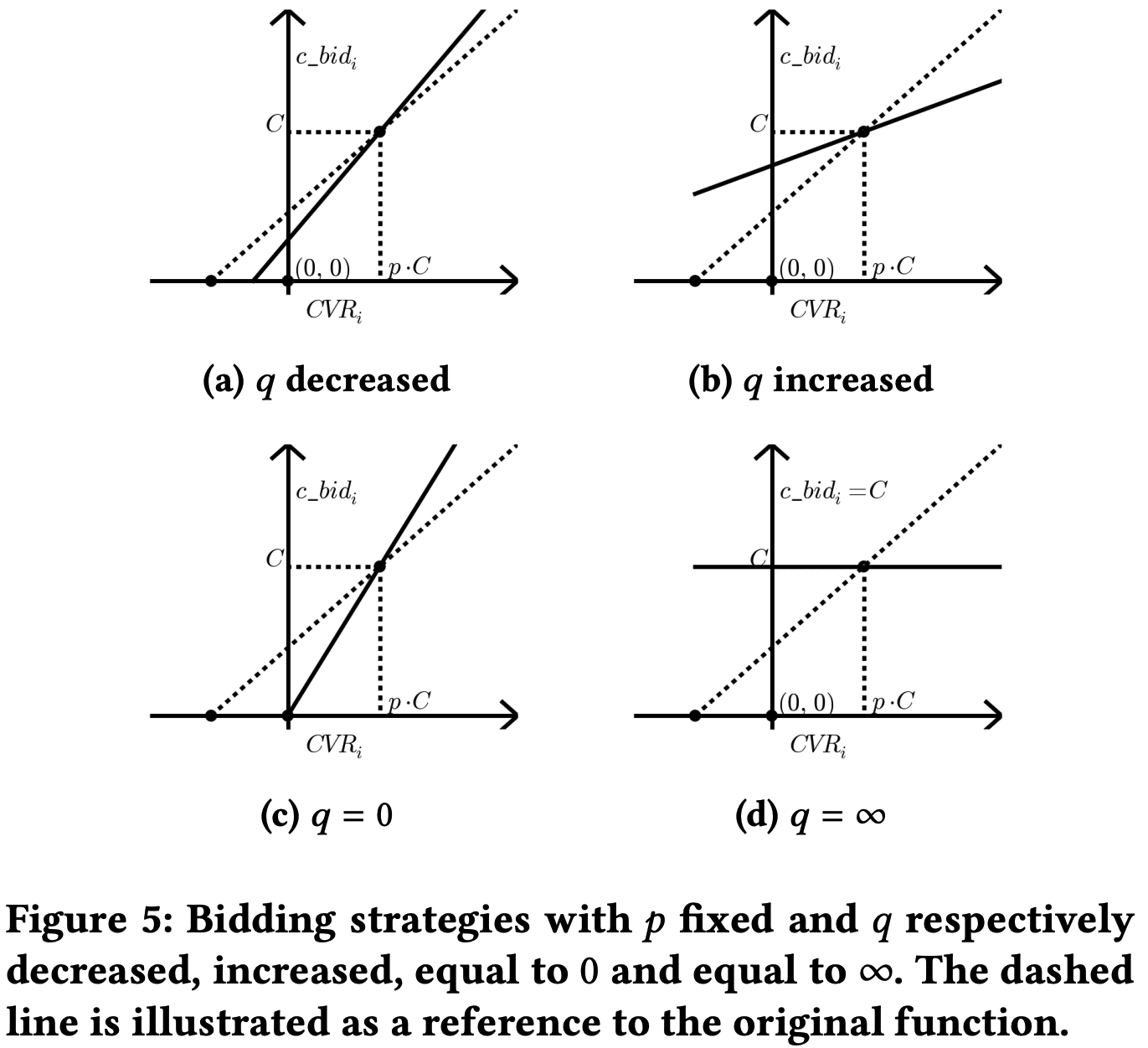
以类似的方式，论文固定 $p$ 并将 $q$ 分别设为减小、增大、等于0和等于 $\infty$ 。如图5所示， $q$ 对最优竞价策略的影响与 $p$ 的影响显著不同
- 当论文增加 $q$ 时 ，竞价策略将围绕点 $(p \cdot C, C)$ 顺时针旋转。增加 $q$ 时，高于 $C$ 的竞价价格将降低，低于 $C$ 的竞价价格将提升。因此，广告 campaign 将赢得更多CPC低于 $C$ 的广告机会，而减少CPC高于 $C$ 的广告机会。综合结果是CPC更有可能低于 $C$ 。在极端情况下，当 $q = \infty$ 时，CPC将保证低于 $C$ 。当 $q$ 设为0时，意味着CPC约束被移除，竞价策略由 $p$ 决定 ，并退化为（Perlich等，2012；Zhang等，2016）中的最优预算约束竞价策略。基于分析，论文声称CPC可以通过 $q$ 明确控制。论文提出以下两个陈述：
  - 1）超参数 $p$ 对预算支出具有直接和有效的控制能力，并且在任何 $q$ 值下，预算支出速度都可以通过 $p$ 明确降低
  - 2）超参数 $q$ 对CPC具有直接和有效的控制能力，并且在任何 $p$ 值下，CPC约束都可以通过调整 $q$ 明确实现

多变量控制

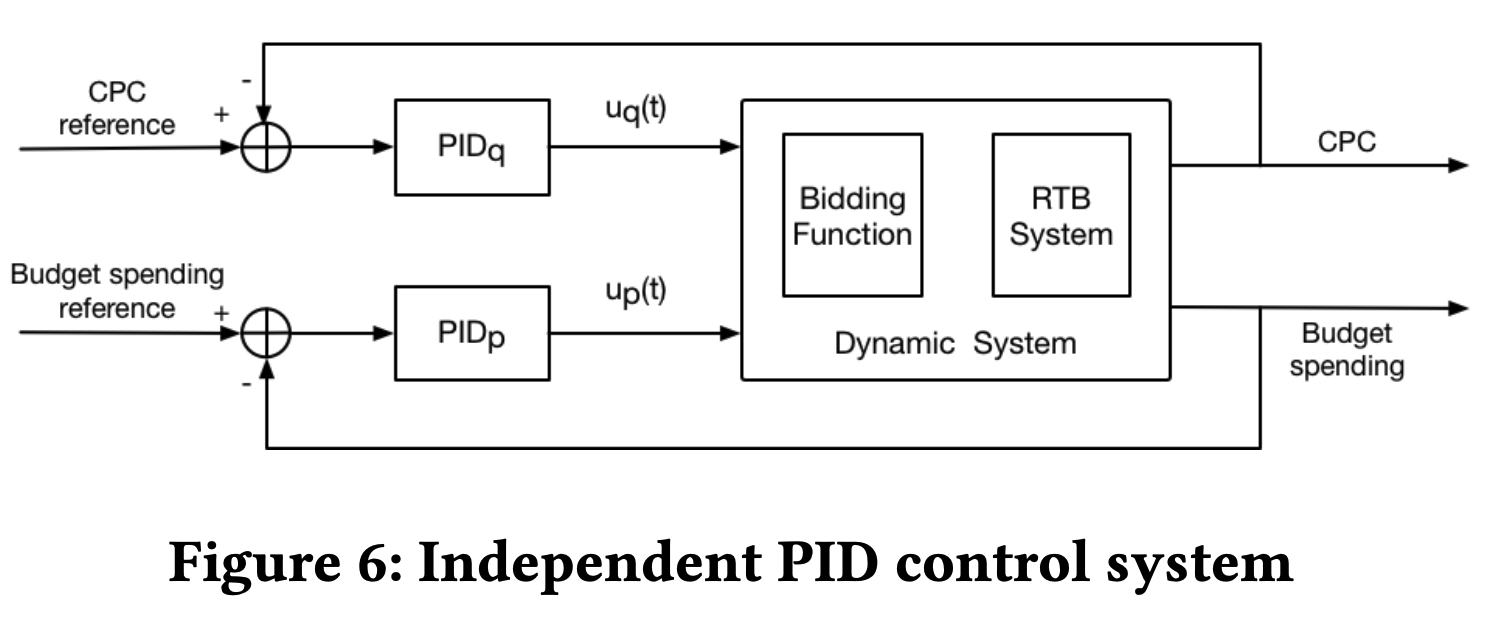
如上一节所述，预算支出和CPC可以分别通过 $p$ 和 $q$ 明确控制。换句话说， $p$ 和 $q$ 可以用于独立控制预算支出和CPC，并将彼此视为外部噪声。因此，我们可以将多变量反馈控制问题分解为两个单变量反馈控制问题。通过这样做，PID控制器可以轻松部署，论文提出了图6中的独立PID设计，其中论文稍微滥用下标 $p$ 和 $q$ 以区分两个控制器
进一步，论文重新审视之前的分析。如图4所示，增加 $p$ 通常会降低竞价价格并减少预算支出速度。增加 $p$ 引起的另一个 non-trivial 影响是预期CPC也会降低。根据这些观察，调整 $p$ 实际上会对CPC产生影响。类似地，调整 $q$ 也会对预算支出产生了影响。尽管论文的独立PID控制系统可以处理这种耦合效应（控制器将其视为外部噪声），但通过解决此类问题，可以进一步提高系统的性能。然而，由于论文对动态系统没有明确的了解，这种耦合效应难以量化和补偿
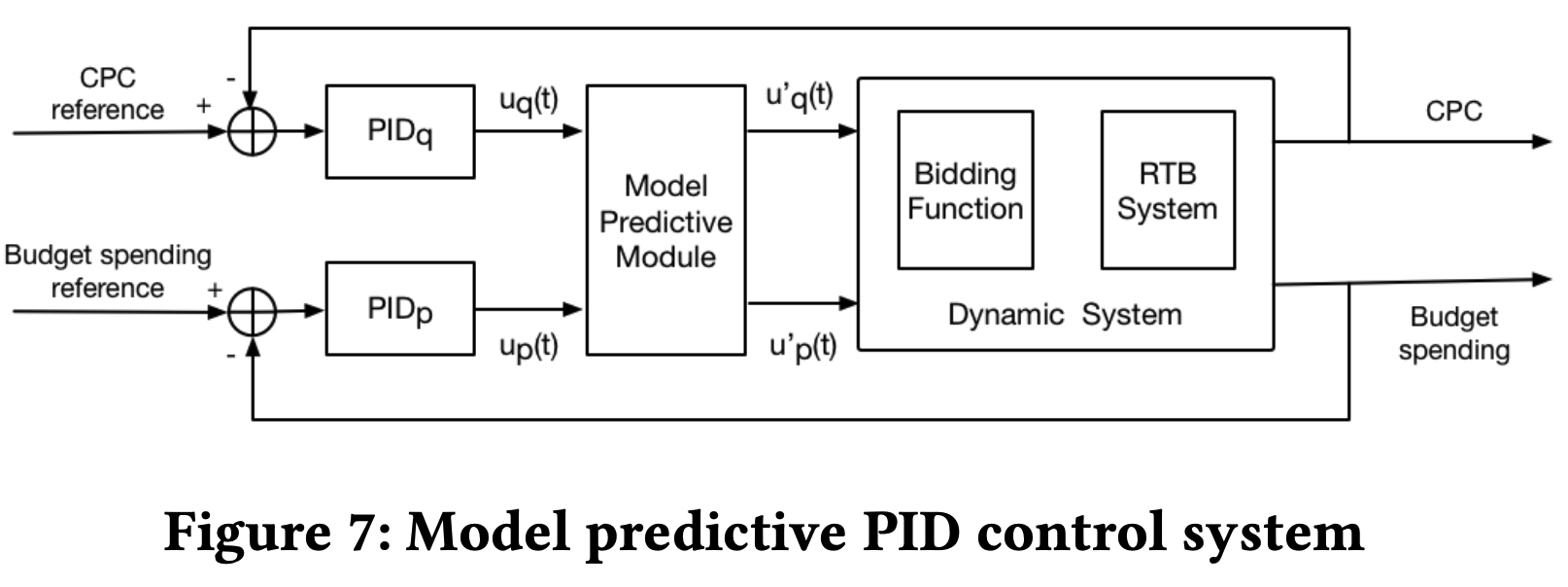
为了解决上述问题，论文利用模型预测控制（MPC）（Rawlings和Mayne，2009）的基本思想来预测和补偿耦合效应。值得注意的是，论文没有直接在控制系统中应用MPC ，因为建模高度非线性的RTB环境成本高昂甚至不切实际。在论文的设计中，结合人类知识，模型预测模块仅需预测耦合效应，这可以通过线性模型近似。如图7所示，在PID控制器之后部署了一个模型预测模块，通过解决耦合效应来调节控制信号
MPC最重要的组成部分之一是表示动态系统行为的模型。在论文的案例中，论文针对成本和CPC对竞价环境进行建模：
- 如公式（16）所示，其中 $\mathbf{X}$ 是一个 $2 \times 2$ 矩阵， $\mathbf{b}$ 是一个 $2 \times 1$ 矩阵
- 在从反馈中获得预期的 $\Delta cost$ 和 $\Delta CPC$ 后，我们可以通过求解公式（17）中的方程来调整 $p$ 和 $q$ ，并推导出如公式（18）所示的结果
- 公式（18）表明， $p$ 和 $q$ 的控制信号应该是成本和CPC变化的线性组合
- 因此，论文通过公式（19）定义模型预测模块：
  - 其中 $\Delta cost$ 和 $\Delta CPC$ 分别由 $u_p(t)$ 和 $u_q(t)$ 量化，
  - 而 $[\mathbf{X}]^{-1}$ 由 $\alpha$ 和 $\beta$ 确定的 $2 \times 2$ 矩阵近似
  - 通过近似 $[\mathbf{X}]^{-1}$ ，我们可以简单地将 $\alpha$ 和 $\beta$ 视为两个权重参数，并在训练集中搜索其最佳值
    - 尽管这种近似削弱了表示系统的能力，但它使控制器在变化的环境中更加鲁棒和稳定
    - 问题： $\alpha$ 和 $\beta$ 的最佳值如何搜索？是类似PID的参数 $K_p,K_i,K_d$ 等一样搜索吗？
- 值得注意的是，论文提出了矩阵 $\mathbf{X}$ 和 $\mathbf{b}$ 来建模动态系统，然而，这些矩阵的确切值并不明确需要。如公式（19）所示，论文利用这些矩阵来解决耦合效应，并获得仅由 $\alpha$ 和 $\beta$ 确定的近似函数

$$\begin{bmatrix}
cost \\
CPC
\end{bmatrix}
=
\begin{bmatrix}
\mathbf{X} & \mathbf{b}
\end{bmatrix}
\begin{bmatrix}
p \\
q \\
1
\end{bmatrix}
\tag{16}$$

$$\begin{bmatrix}
\Delta cost \\
\Delta CPC
\end{bmatrix}
=
\begin{bmatrix}
\mathbf{X}
\end{bmatrix}
\begin{bmatrix}
\Delta p \\
\Delta q
\end{bmatrix}
\tag{17}$$

$$\begin{bmatrix}
\Delta p \\
\Delta q
\end{bmatrix}
=
\begin{bmatrix}
\mathbf{X}
\end{bmatrix}^{-1}
\begin{bmatrix}
\Delta cost \\
\Delta CPC
\end{bmatrix}
\tag{18}$$

$$\begin{bmatrix}
u’_p(t) \\
u’_q(t)
\end{bmatrix}
=
\begin{bmatrix}
\alpha & 1 - \alpha \\
1 - \beta & \beta
\end{bmatrix}
\begin{bmatrix}
u_p(t) \\
u_q(t)
\end{bmatrix}
\tag{19}$$

实证研究

在本节中，论文进行了全面的实验，以证明论文的陈述和多变量控制系统的优势
论文在示例广告 campaign 上进行了实验，以证明超参数的控制能力
为了展示论文系统的优越性，论文在大量广告 campaign 上将论文的方法与行业最新实践进行了比较

Experiment Setup

数据集

论文基于淘宝网的真实数据集进行实验。数据集包含40个广告 campaign 在连续多天的数据，总计2000万条竞价日志。根据日期将其分为训练数据集和测试数据集。从特定广告 campaign 的角度来看，数据集的关键信息可以总结为表1
论文主要使用获胜价格、CTR和CVR的信息。每个广告机会的获胜价格在每次在线拍卖结束后记录。由于淘宝网也是一个发布商，即使广告主在在线拍卖中错过了广告机会，也可以观察到获胜价格。CTR和CVR由在线部署的模型估计，这些模型利用了用户和广告的广泛实时和历史信息。有关在线部署的估计模型的详细信息，请参阅（Zhou等，2018）

指标

竞价策略和系统的目标是最大化赢得广告机会的总价值，并将CPC控制在给定阈值以下。论文通过 $CTR \cdot CVR$ 的总和量化广告价值，这对应于转化的预期结果。值得注意的是，论文将 $CTR \cdot CVR$ 视为价值，而非实际转化事件，以排除估计模型不准确带来的影响（注：尽管一些先前的工作通过实际转化评估竞价策略，但作者认为估计误差实际上对结果产生了 non-trivial 影响）。所以，具有固定竞价策略的广告 campaign 可能仅通过优化估计模型就获得更多点击/转化，因此论文将 $CTR \cdot CVR$ 视为真实转化以减少这种影响
- (1) $R$ 表示广告 campaign 的广告价值
- (2) $R^*$ 表示广告 campaign 在预算和CPC约束下可以实现的最高广告价值
- (3) $R/R^*$ 可用于评估广告性能与理想结果的接近程度
- (4) $CPC_{ratio}$ 是满足CPC约束（允许10%的超调）的广告 campaign 比例，可用于在大量广告 campaign 上比较不同方法时评估CPC控制能力
- (5) $Value_{ratio}$ 是在CPC约束成立的广告 campaign 上的平均 $R/R^*$ ，用于评估广告价值的实现。对于那些打破CPC约束的广告 campaign ，论文在计算 $Value_{ratio}$ 时排除了它们的 $R/R^*$ ，因为在论文的场景中，通过打破CPC约束赢得更多价值是不允许的

实现细节

论文在PID控制器和基线策略中采用了公式（20）所示的执行器，其中 $u(t)$ 的符号取决于输入参数和输出变量之间的关系
$$x(t+1) = x(0) \cdot \exp(-u(t)) \tag{20}$$
此外，需要注意的是，论文实际上关心的是广告 campaign 结束时的累计CPC，而每个时间步的实时CPC对累计CPC的贡献不同，因为每个时间步的点击量不同。传统的PID误差无法解决论文场景中的不同权重问题，因此论文通过点击量对误差进行加权，并修改 $q$ 的控制信号，如公式（21）和公式（22）所示，其中 $u(t)$ 由公式（14）计算， $click(t)$ 表示时间步 $t$ 的点击量。通过这种修改，PID控制器将不断增加其对累计CPC的关注，并为每个时间步赋予不同的权重：
$$e_q(t) = click(t) \cdot (r(t) - y(t)) \tag{21}$$

$$u_q(t) = \frac{1}{\sum_{i=1\ldots t}^T click(t)} \cdot u(t) \tag{22}$$

$$u(t) = k_p e(t) + k_i \sum_{k=1\ldots t} e(k) + k_d (e(t) - e(t-1)) \tag{14}$$

针对上述公式的理解：
- $e(t) = click(t) \cdot (r(t) - y(t))$ 表示当前时间片 $t$ 的累计收入差异（注意：这样得到的是目标消耗和真实消耗的差异）
  $$
  \begin{align}
  e(t) &= click(t) \cdot (r(t) - y(t)) \\
  &= click(t) \cdot (\frac{targetCharge(t)}{click(t)} - \frac{realCharge(t)}{click(t)}) \\
  &= targetCharge(t) - realCharge(t)
  \end{align}
  $$
- 从上面的推导进一步可以得到，经过这样处理的后的积分项 $\sum_{k=1\ldots t} e(k)$ 表示全天截止到当前目标消耗与真实消耗的差异，在一些无法分时间片做特征的场景中，可以用这一项去替换这个值
  - 补充思考 ：考虑到越到后面，积分项影响越大，比例项影响越小，真实场景中如果没有的话，甚至可以不使用比例项
为了确定PID控制器的权重参数以及权重参数 $\alpha$ 和 $\beta$ ，论文在训练数据集上网格搜索最佳设置，并将其应用于测试数据集。论文将每小时视为一个时间步，因此最大时间步 $T$ 等于24
参考值设定 ：如论文在前面章节中讨论的，PID控制器需要一个参考值（目标值）。在论文的实验中，广告主给出的CPC被设为控制 $q$ 的恒定参考值。考虑到广告机会和获胜价格对成本有直接影响，并且在时间步上表现出不同的统计特征，成本参考值应根据时间步定制（如果目标就是全天达到商家的某个固定目标值呢？）。论文计算训练数据集上的成本分布，即每天每个时间步的理想成本归一化为总成本，作为成本参考
论文的实验流程步骤如下：
- 1）在训练数据集上计算最优的 $p$ 和 $q$ ；
- 2）在测试数据集上模拟竞价过程，其中计算出的 $p$ 和 $q$ 作为初始超参数应用；
- 3）当广告 campaign 预算耗尽或没有更多广告机会时，模拟结束

控制能力

在本节中，论文进行实验以证明论文的陈述，即预算支出和CPC可以分别通过 $p$ 和 $q$ 独立控制。论文同时调整两个超参数，而不使用模型预测模块，并在示例广告 campaign 上分别展示预算支出和CPC的控制性能。控制性能如图8和图9所示：
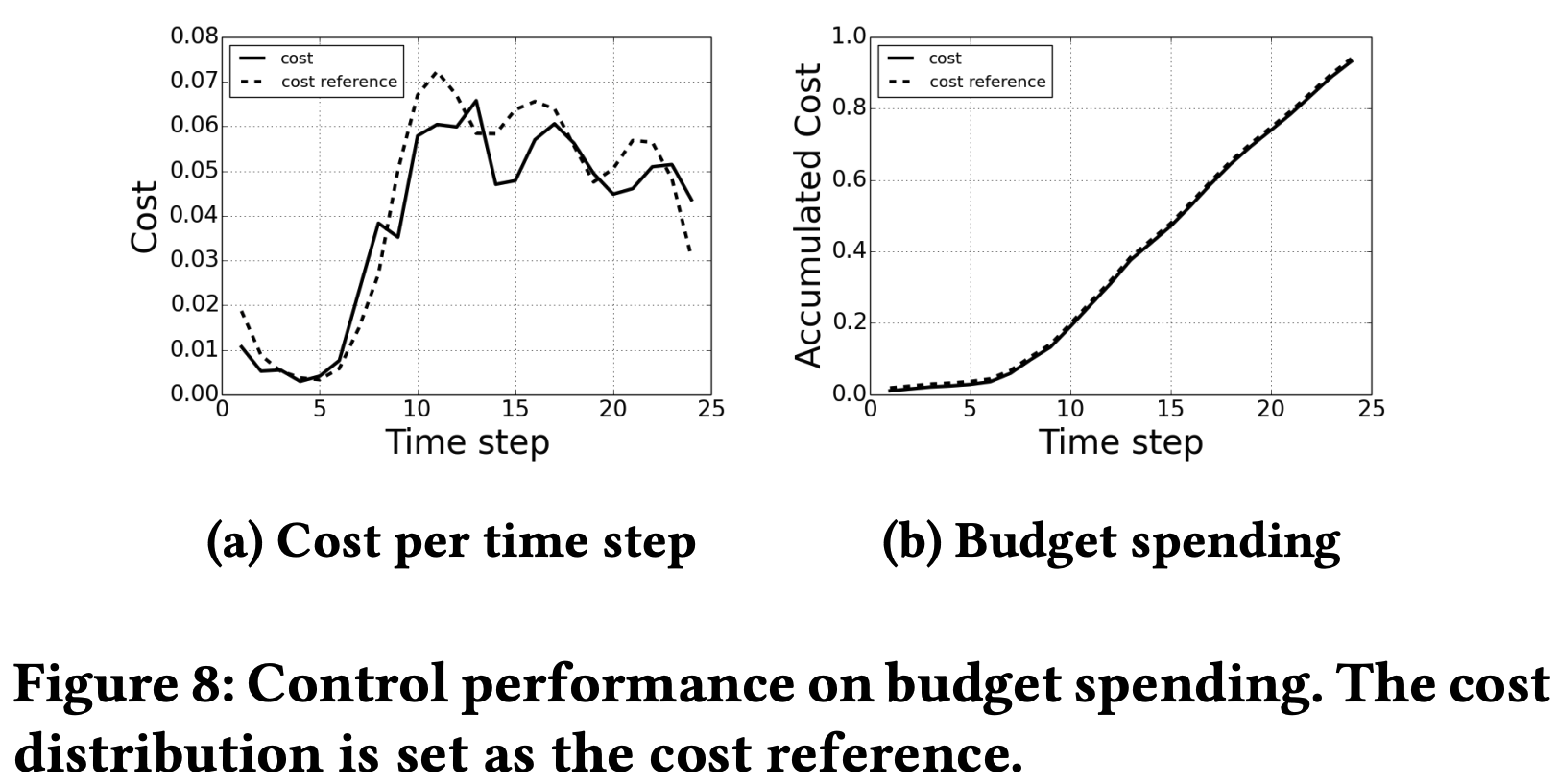
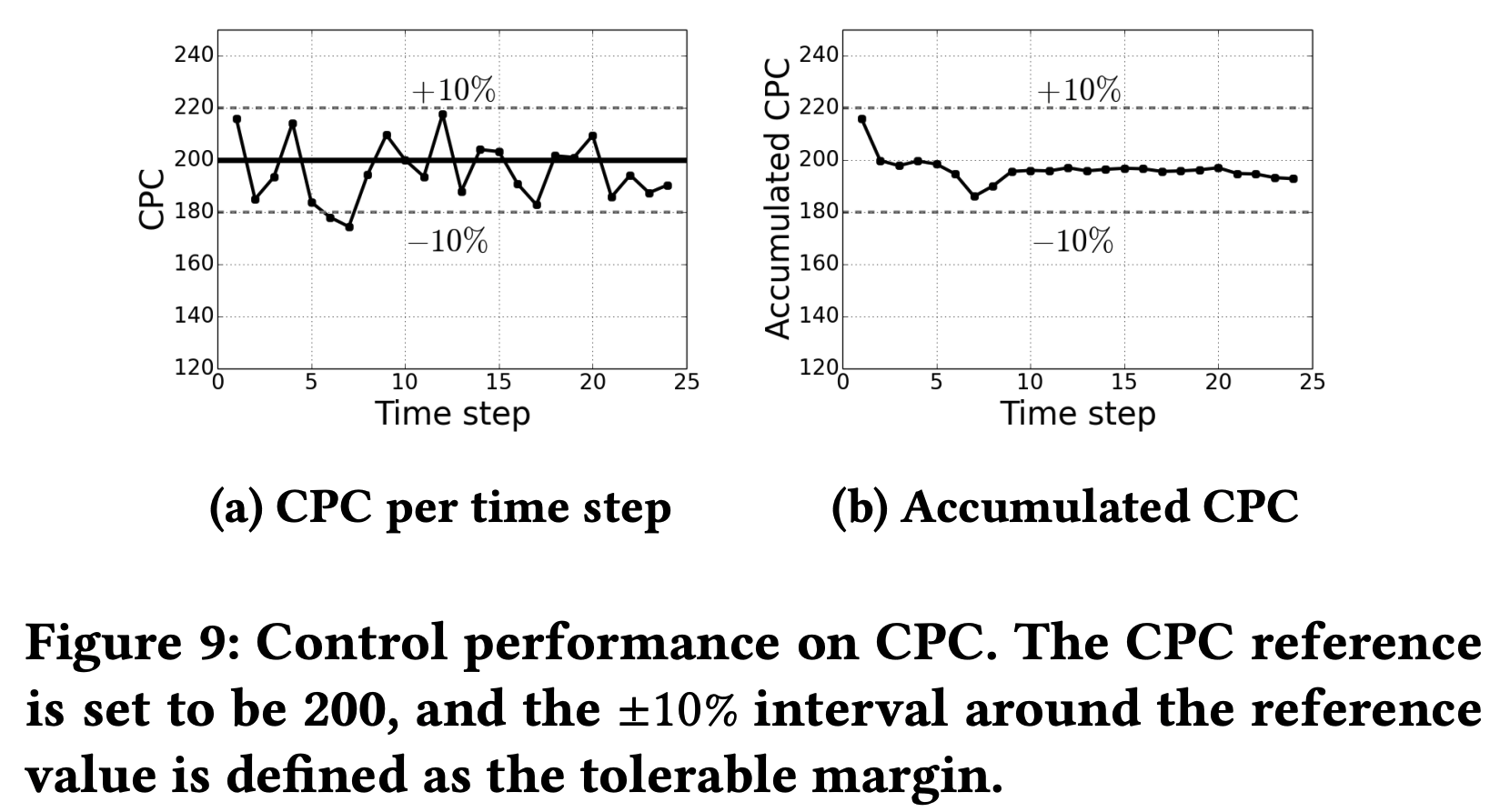
如图8所示，由 $p$ 控制的每个时间步的成本围绕成本参考值波动，累计成本相对于累计成本参考值得到了良好控制。如图9所示，每个时间步的CPC迅速被限制在可容忍的范围内，累计CPC成功控制在给定的参考值以下。值得注意的是，实时CPC在时间步上表现出可观察的波动，因为论文对实时CPC的关注逐渐减少（因为积分项的影响会逐渐增大）。与实时CPC相比，累计CPC表现出稳定的性能，如图9b所示。根据实验，尽管 $p$ 和 $q$ 相互干扰，但它们可以独立调整以控制相应的输出变量

性能评估

在本节中，论文将论文的方法与行业最新实践进行比较。论文首先介绍基线策略，并在真实数据集上评估它们

基线策略

Cost-min ：Cost-min（Kitts等，2017）是一种在广告场景中解决多约束的通用算法，可以应用于论文的场景如下。采用竞价策略公式（23）。论文通过PID控制器根据成本参考值调整 $b_0$ ，并将 $c\_bid_i$ 的上限设为 $C$ 。由于截断的竞价价格，广告 campaign 的CPC约束将始终成立。论文将给定的CPC除以广告 campaign 所有竞价日志的平均CVR来初始化 $b_0$
$$ c\_bid_i = b_0 \cdot CVR_i \tag{23} $$
Fb-Control ：Zhang等提出了一种动态调整竞价以控制CPC的反馈控制机制（Zhang等，2016）。在他们的工作中，他们采用了广义竞价策略，如公式（24）所示，并通过PID控制器根据CPC的反馈不断调整 $b_0$ 。给定的CPC被设为 $b_0$ 的初始值。为简单起见，论文将他们的方法称为Fb-Control
$$ c\_bid_i = b_0 \tag{24} $$
Fb-Control-M ：Fb-Control没有考虑点击的价值（即CVR），这对提高广告性能很重要。因此，论文修改了他们的竞价策略以更好地适应论文的场景，如公式（23）所示，其中 $b_0$ 通过PID控制器根据论文的成本参考值进行调整，而 $c\_bid_i$ 的上限通过独立的PID控制器根据CPC的反馈进行控制。上限由给定的CPC初始化，将在每次竞价时截断 $c\_bid_i$

评估结果

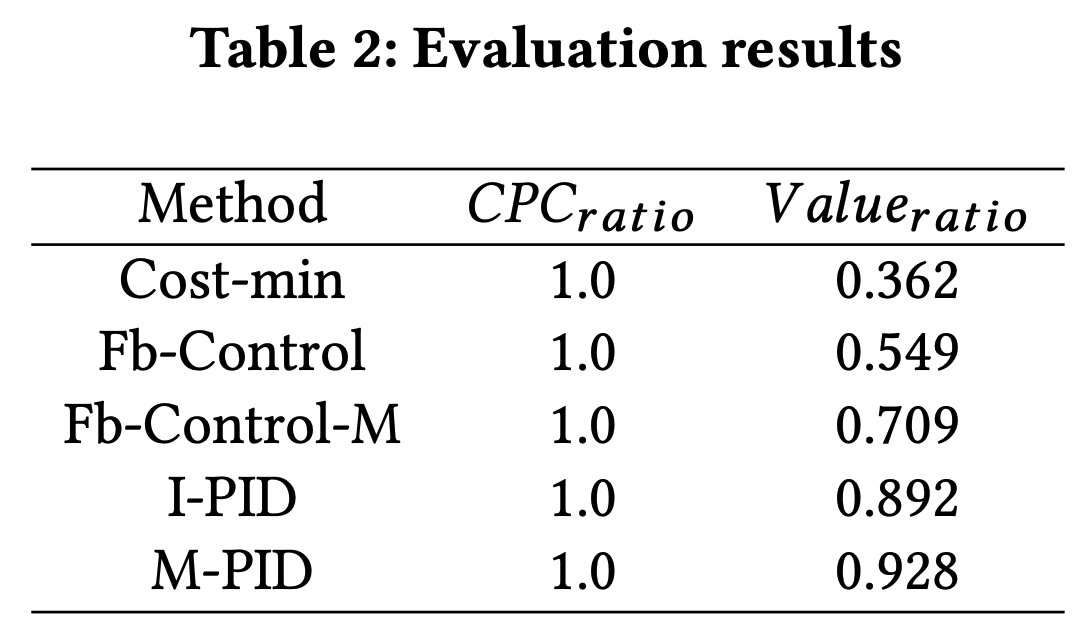
论文在40个广告 campaign 上评估了所有方法，并计算了 $CPC_{ratio}$ 和 $Value_{ratio}$ 。结果总结在表2中。从表2可以看出，所有方法都能成功控制CPC，因为它们的 $CPC_{ratio}$ 均为1.0。然而，论文的方法在广告价值实现方面显著优于基线策略。具体来说，独立PID控制系统（I-PID）和模型预测PID控制系统（M-PID）分别实现了0.892和0.928的 $Value_{ratio}$ ，而最佳基线策略Fb-Control-M仅实现了0.709。此外，M-PID的性能优于I-PID，这表明模型预测模块通过解决耦合效应进一步提高了系统的性能

附录：相关工作（原文直译）

注：为方便check，这里均保留引用信息

论文的工作与在线广告中的竞价策略和反馈控制密切相关。在线广告中的竞价策略已被广泛研究（Wang和Yuan，2015）。Zhang等（Zhang等，2014）提出了一种在预算约束下最大化点击量的最优竞价策略。Perlich等（Perlich等，2012）提出了一种基于库存评分的竞价策略。Lee等（Lee等，2013）提出了一种在预算平滑约束下的实时竞价优化方法。Zhang等（Zhang等，2016）提出了一种广义竞价策略，并通过反馈控制机制动态调整竞价以控制CPC。论文的工作与他们的不同之处在于，论文同时考虑了预算和KPI约束，并推导出最优竞价策略
馈控制在在线广告中的应用也得到了广泛研究（Karlsson和Zhang，2013）。Jamali等（Jamali等，2012）提出了一种基于控制理论的推荐系统。Zhang等（Zhang等，2016）提出了一种基于反馈控制的竞价策略。论文的工作与他们的不同之处在于，论文设计了一个多变量控制系统，以同时控制预算支出和CPC
此外，论文的工作还与线性规划和 primal-dual 方法相关。线性规划已被广泛应用于在线广告中的资源分配问题（Agrawal等，2014）。 primal-dual 方法已被用于解决在线线性规划问题（Buchbinder等，2007）。论文的工作与他们的不同之处在于，论文采用这种方法推导最优竞价策略而非分配策略。为了解决动态环境问题，论文利用了反馈控制理论，该理论已被许多工作证明在多种场景中有效（Jamali等，2012；Karlsson和Zhang，2013；Zhang等，2016）。其他相关工作包括点击率估计（McMahan等，2013；Zhou等，2018）、转化率估计（Lee等，2012；Yang，2017）、获胜价格预测（Wang等，2016；Wu等，2018）和预算平滑（Xu等，2015；Song等，2017）。