- 参考文献:Google KDD 2013,Ad Click Prediction: a View from the Trenches(引用量500+)
- 介绍了截止到2013年之前的点击率预估常用算法,FTRL是Google三年的结晶(2010-2013)
- 在线学习优化算法的发展历程:SGD->TG->FOBOS->RDA->FTRL-Proximal
核心贡献
- 基于传统的逻辑回归算法(Regularized Logistic Regression,正则化的逻辑回归)在点击率预估时的不足,提出一种在线逻辑回归算法,FTRL(Follow The Regularized Leader)
- per-coordinate learning rate
一些模型的比较和介绍
- 传统逻辑回归算法中使用OGD(Online Gradient Descent)是非常高效的,使用很小的计算资源就能得到较好的精确度.
- 但是OGD在生成稀疏模型方面表现不好(OGD + L1)
- 其他在稀疏性方面表现良好的方法有FOBOS, 截断梯度(Truncated Gradient)和 RDA(Regularized Dual Averaging)
- RDA在精确度和稀疏性方面做tradeoff, 效果好于FOBOS
- FTRL-Proximal号称可以同时获得RDA的稀疏性和OGD的精确度
- RDA模型是微软提出的一种在线优化算法,与OGD完全不同,能得到更加稀疏的模型,但是精确度不如OGD
FTRL-Proximal Learning (Online Learning And Sparsity)
- 也是通过L1正则化控制模型的稀疏度
推导过程
FTL(Follow The Leader)的介绍
OGD的更新方式
- 更新规则:
$$
\begin{align}
\mathbf{w}_{t+1} &= \mathbf{w}_t-\eta_t\mathbf{g}_t
\end{align}
$$
FTLR(Follow The Regularized Leader)
加上正则项的FTL
- 更新规则:
$$
\begin{align}
\mathbf{w}_{t+1} &= \mathop{\arg\min}_{\mathbf{w}}\left ( \mathbf{g}_{1:t}\cdot \mathbf{w} + \frac{1}{2}\sum_{s=1}^t \sigma_s || \mathbf{w} - \mathbf{w}_s||_2^2 + \lambda_1||\mathbf{w}||_1 \right ) \\
\mathbf{g}_{1:t} &= \sum_{i=1}^t\mathbf{g}_i
\end{align}
$$- 第一项是对损失函数梯度的贡献的一个估计
- 第二项是控制参数 \(\mathbf{w}\) 在每次迭代中变化不要太大
- 第三项是L1正则化,用于使模型变得稀疏(除了L1正则化项以外,也可以再加上L2正则化)
- 去掉正则化项就是FTL(Follow The Leader)
- \(\sigma_s\) 是学习速率
- 这个学习速率可以用Per-Coordinate Learning Rate:
$$
\begin{align}
\eta_{t, i} &= \frac{\alpha}{\beta + \sqrt{\sum_{s=1}^t g_{s,i}^2}} \\
\mathbf{g}_s &= \nabla l_s(\mathbf{w})
\end{align}
$$
Per-Coordinate Learning Rates
- 对参数的每一维度分开训练,每个维度有自己的学习率
- 某个特征出现的次数越多,说明当前该特征对应的参数值越可信,学习率就应该越小
- 考虑了数据在每个特征上的分布不均匀性
- 参数某个维度上的样本数越少,这些样本就会得到越大的利用(具体表现就是该特征的学习率会比较大)
一个思考
- 问题:为什么机器学习中的学习率都是越来越小?
- 答案:因为刚开始训练时,参数的值不太可信(也就是说最终参数与当前参数的置信度比较低),所以更新时应该更新的步骤大一些,让当前的参数变化大一些,训练到后来,随着参数的值越来越可信(当前参数的置信度比较高),更新的步骤就应该小一些,让当前的变化小一些
一些工程上的Trick
Saving Memory at Massive Scale
Probabilistic Feature Inclusion
- 在高维数据中,大量的特征是出现频率非常低的(rare),半数的唯一特征甚至只出现一次
- 统计这些特征的代价是非常昂贵的,有些特征可能永远不会被实际使用(这里如何理解昂贵?也就是说训练了也没用?)
- 额外的读写数据是昂贵的,如果能丢弃一部分出现评论特别低的特征(比如出现频率低于k次)
- 实现稀疏可以使用L1正则化,也可以使用Probabilistic Feature Inclusion
- 关于Probabilistic Feature Inclusion的做法
- 当一个特征第一次出现时,以一定的概率接受这个新特征
- 效果作用于数据预处理阶段,但是可以在在线执行中设置
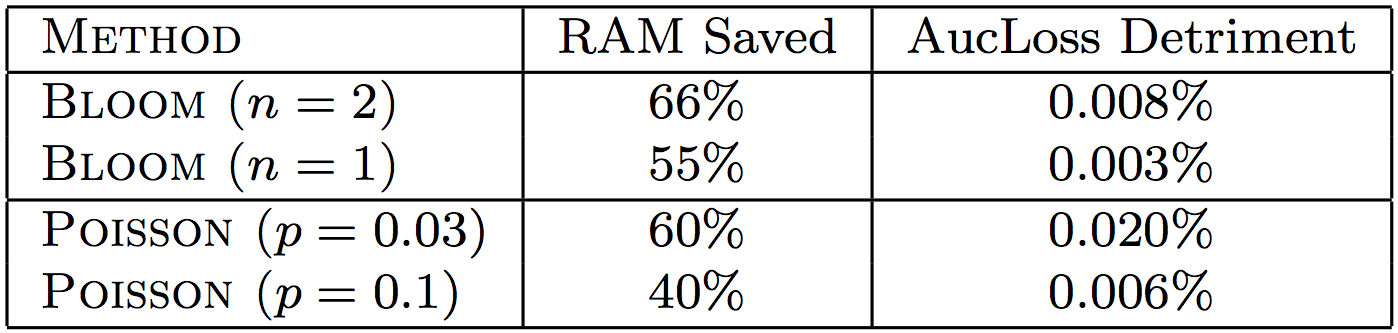
Possion Inclusion
- 对于新的特征,以概率p添加入模型
- 对于已经存在模型中的特征,正常更新其系数
Bloom Filter Inclusion
- 用布隆过滤器仅仅保留出现次数在n次以上的特征
Encoding Values with Fewer Bits
- 常用的OGD使用32或者64位浮点数编码来存储模型的系数
- Google提出可以使用16位浮点数来存储系数,同时加上一些策略
- 实验结果:将64位的浮点值换为为系数存储节省了75%的RAM内存空间(这还用实验?直接计算就得到了啊)
Training Many Similar Models
- 同时训练多个模型是超参数选择常用的方法
- 将可以共享的东西共享
- 在节省内存的同时,还可以节约网络带宽(存储一份Per-coordinate学习率,节省内存和带宽等),CPU(用同一个hash表检索特征,节省CPU)和硬盘空间
A Single Value Structure
- 有时候我们希望评估大量的模型在只有少量的特征组(groups of features)添加或者删除时的变化
- 对于每一维度(coordinate),仅仅存储一个系数值而不是多个(正常应该为每个模型存储一个)
- 存储该维度对应特征组的模型共享该系数
- 对每个特征,训练时每个模型都会计算自己的值,然后所有模型的取平均作为所有包含该维度特征模型的共享
Computing Learning Rates with Counts
- 对于每个特征来说,梯度和以及梯度平方和是必须计算的
- 梯度的计算必须准确,但是计算学习率却是可以粗糙计算的
- 仅仅统计样本出现次数(Counts)就能大概计算学习率
推导
- 假设包含一个给定特征的所有事件(events)具有有相同的概率(一般来说,这个近似是不可能的,但是在这个目标里面是可行的)
- 如何理解这个假设的意义呢?*对于具有某个特征的所有样本,其取值为(正负例)是的概率是相等的,正例(click)概率都为 \(p\) *
- 进一步假设模型已经精确地学习到了概率
- 如果有分别有 \(P,N\) 个正负样本(events),则有 \(p=\frac{P}{N+P}\)
- 则有对于逻辑回归(\(p(1-p)\))来说,正例的梯度为 \(p-1\),负例的梯度为 \(p\)
$$
\begin{align}
\sum g_{t,i}^2 &= \sum_\text{positive events}(1-p_t)^2 + \sum_\text{negative events}p_t^2 \\
&\approx P(1-\frac{P}{N+P})^2 + N(\frac{P}{N+P})^2 \\
&= \frac{PN}{N+P}
\end{align}
$$ - 也就是说,为了近似计算 \(\sum g_{t,i}^2\),我们仅需要记录 \(P,N\) 即可
Subsampling Traning Data
- 典型的CTRs是远远低于50%,数据偏差很大,正例(点击)的样本很稀疏
- 在模型训练中正例样本相对而言更有价值
- 使用下采样:很大程度上降低数据量,同时保证对精度最小程度的影响
采样方法:
- 保留所有至少被点击过一次的请求(Query,也就是样本)
- 以一定比例 \(r\in(0, 1]\) 采样没有被点击过的请求
- 因为包含通用的特征(Feature Phase)计算,所以这种方法是合理的,但是需要纠偏(直接用采样后的样本训练会造成预测偏差)
- 加入一个重要性权重 \(w_t\)
- \(w_t = 1\) for clicked queries
- \(w_t = \frac{1}{r}\) for queries with no clicks
- 本质上可以理解为这里是将采样时造成的负例比例偏差补齐
模型性能评估
Progressive Validation
- Progressive验证又称为在线损失(online loss)
- 与交叉验证(cross-validation)或留出法(hold out)验证是不同的
- 在服务查询中,在线损失能很好的代表我们的精度,因为在训练模型前,它仅仅在最新数据上评估其性能(因为这准确的模拟了当模型进行服务查询时发生了什么)
- 由于用了100%的数据作为训练和测试,在线损失比留出法验证有更好的统计数据
- 绝对指标往往会带来误导
- 即使预测是完美的,对数损失和其他指标的差异也依赖着问题的困难程度
- 不同的国家,不同请求的点击率不同(同为对数损失的最佳实践,50%的点击率会好于2%的点击率)
- 所以使用相对变化,看指标相对于base line改变了多少
- 从经验来看,相对指标在整个时间段内都很稳定
- 相同的指标计算应该对应在完全相同的数据(比如不同时段的损失比较是没有意义的)
置信度评估(Confidence Estimates)
- 对很多应用来说,除了评估广告的CTR,还要量化预测的期望精确度(the expected accuracy of the prediction)
校正预测(Calibrating Predictions)
- 系统偏差(Systematic Bias)指平均预测CTR(Average Predicted CTR)和观测CTR(Observed CTR)的差异
- 造成系统偏差的原因包括:
- 不精确的模型假设
- 学习算法的缺陷
- 在训练或者服务(预测)时不可用的隐藏特征
- 解决方案:
- 添加一个校正层将预测CTRs与观测CTR做匹配(match predicted CTRSs to observed click-through rates)
- 暂时不能提供有效的保证,保证校正影响的有效
- 校正的本质是找到(拟合)一个函数映射 \(g\),使得模型输出值与真实概率值一一对应
- 逻辑回归中的sigmoid函数可以看做是一个校正预测的函数吗?
- 更多参考
一些说明
- 概率模型的搭建过程中,由于抽样与正则化等原因,导致模型的输出概率值明显偏离真实概率值
- [待更新:为什么抽样和正则化会影响模型的输出概率发生变化?]
- 此时的模型输出概率值仅仅有排序的意义,其绝对值没有意义(定序值,而非定距数值)
- 校正预测的过程就是把模型输出概率值的校正成真实的概率的过程,使得校正后的概率有绝对值意义
自动特征管理(Automated Feature Management)
- 将特征空间描绘成上下文和语义信号,每个信号都可以被翻译成一个在学习时有真实值的特征集合
- [待更新]
一些不成功的实验记录(Unsuccessful Experiments)
本节记录google的一些失败的尝试方向(有些可能会让人很惊讶),这些方向模型没有明显收益
Aggressive Feature Hashing
关于特征哈希(Feature Hashing)的相关知识可参考Feature-Hashing
- Feature Hashing for Large Scale Multitask Learning论文指出,Feature Hashing方法效果显著
- 报告显示使用特征hashing技巧,可以能将学习一个垃圾邮件过滤模型的特征空间映射成包含 \(2^24\) 个特征的特征空间(疑问:这里的特征原来不止 \(2^24\) 个吗?)
- 但是实验证明,使用 Feature Hashing 方法并不能提升我们的方法,所以建议保留 interpretable(non-hashed)的特征向量
Dropout
- Google用网格搜索的方法测试了从0.1到0.5的Dropout特征丢弃概率
- 所有情况均没有带来任何收益(包括精度指标和泛化能力),还往往给模型带来损害(detriment)
- Google给出的一个解释是:Dropout在图像领域取得较好收益的原因是因为图像领域的数据特征分布与计算广告领域不同
- 图像领域:稠密特征,此时Dropout把结果(effect)从强相关的特征中分离开来,从而得到泛化效果更好的分类器
- 计算广告:稀疏特征,且有噪音
Feature Bagging
- 对特征进行overlapping采样(注意,样本Bagging和特征Bagging不同),然后训练多个独立的模型,最后取平均值
- 实验证明模型的的AucLoss降低了0.1%-0.6%
Feature Vector Normalization
- \(\mathbf{x} = \frac{\mathbf{x}}{||\mathbf{x}||}\)
- 开始有一点精度上的收益,但是后面也出现了一定程度的detriment
- Google的解释是可能是由于per-coordinate learning rates和正则化的影响