CA——GAVE

参考链接：
- 原始论文：Generative Auto-Bidding with Value-Guided Explorations, SIGIR 2025, Kuaishou

整体思路

现有自动出价方法 ：通常采用 rule-based strategies 或 RL 技术，这些方法存在一些问题：
- rule-based strategies ：缺乏适应时变市场条件的灵活性
- RL-based methods ：在 MDP 框架中难以捕捉重要的历史依赖关系和观测结果
- 通用问题 ：
  - 目前切换的适应性问题 ：在 ensuring strategy adaptability across diverse advertising objectives 方面常常面临挑战
  - Offline问题 ：随着越来越多地采用离线训练方法来促进稳定在线策略的部署和维护，在固定离线数据集上进行训练所导致的行为模式记录和行为崩溃问题变得日益突出
为解决这些局限性，论文提出了基于价值引导探索的离线生成式自动出价框架（offline Generative Auto-bidding framework with Value-Guided Explorations，GAVE）
- 通过 Score-based未来回报（Return-To-Go, RTG）模块适应各种广告目标
- 将动作探索机制与基于 RTG 的评估方法相结合，在探索新动作的同时确保保持稳定性的更新
- 设计了一个可学习的价值函数来指导动作探索的方向，并减轻 OOD（Out-of-Distribution）问题
实验：离线+在线
- 注：论文方法在 NeurIPS 2024 竞赛 “AIGB赛道 ：使用生成模型学习自动出价智能体” 中荣获第一名
其他：实现代码已开源 Applied-Machine-Learning-Lab/GAVE

一些讨论

自动出价的重要性 ：自动出价凭借其在动态竞争的在线环境中优化出价决策的强大能力，已成为广告平台的关键策略，有助于企业触达目标受众并提高销售额
出价需求 ：现代广告系统非常复杂（市场条件的波动、用户行为的多样性），这要求出价策略能够适应这些变化并与广告商的多样化目标保持一致。此外，大量需要实时处理的广告竞价进一步加剧了这一需求，在这种情况下，人为干预既不切实际，也往往无法实现最佳广告效果
现有解决方案主要发展为两类：
- rule-based strategies ：计算量小且易于部署，但其静态特性导致其不适合动态市场，也无法满足广告商的多样化需求
- RL-based methods ：虽然采用 MDP 来适应环境变化并获得更好的性能，但面临一个关键的结构性制约：
  - MDP 状态独立性假设本质上忽略了出价序列中的时间依赖关系和观测结果。这一限制阻碍了对不断变化的行为模式和市场波动的识别，大大削弱了RL在高度波动的实时出价环境中的实际适用性
  - 个人理解：这里对 RL 无法建模波动主要体现在无法预知快速变化的流量趋势（特别是与历史趋势不一致时）；特别地，出价场景可能是 POMDP 问题，常规 RL 方法将难以解决问题，将历史序列都作为输入才能缓解
DT 在出价上的前景 ：Decision Transformer（DT）作为一个强大的框架，能够有效捕捉时间依赖关系和历史上下文（temporal dependencies and historical context），因此，将 DT 应用于离线出价建模为改进策略提供了一个有前景的方向，其优点有：
- 适配Offline RL场景 ：通过采用离线训练范式，DT 规避了在线训练的风险和实施挑战，确保了在各种场景中的更广泛适用性
- 时间依赖和上下文建模 ： DT 的生成式建模基础进一步使其能够明确捕捉时间依赖关系和历史出价上下文，实现与现实世界广告环境的动态特性相匹配的自适应决策
DT 的面临问题 ：
- 首先，实际部署需要适应复杂的广告目标 ：其评估指标不仅限于总点击量或转化率等基本指标，这些目标通常涉及许多复杂函数（包含相互依赖的参数，如 CPA 或 CPC 约束等），这要求 DT 建模具有自适应优化目标 ，以符合多样化的运营标准
- 其次，在离线环境中直接训练 DT 模型可能会局限于已记录的行为模式 ，并遭受行为崩溃问题，这需要在稳定更新的同时加强动作探索
论文提出了一个统一框架 GAVE，用于增强 DT 在离线生成式自动出价中的应用
- 首先，为适应复杂的广告目标，论文设计了一个 Score-based RTG 模块，其分数函数可定制，通过可微编程实现对各种目标要求（如CPA约束）的自适应建模
- 其次，提出了一种动作探索机制以及基于 RTG 的评估方法，用于在固定数据集之外探索和评估动作，同时确保探索动作与原始动作之间的稳定更新
  - 在如此敏感的出价环境中，动作空间大，通过随机探索学习有益策略并避免分布外（OOD）风险颇具挑战。因此，论文引入了一个可学习的价值函数来指导动作探索过程，将探索导向潜在的最优动作。该机制将探索锚定在合理区域内，同时实现可控的外推（extrapolation），从而促进策略改进并进一步减轻OOD问题
论文的贡献：
- 引入了创新框架 GAVE ，利用 DT 优化自动出价策略，旨在无缝适应各种现实场景，提出了三项技术创新：
  - （1）一个 Score-based RTG 模块，通过可微编程实现针对各种广告目标的可定制函数；
  - （2）一种动作探索机制，结合基于 RTG 的评估，确保稳定更新；
  - （3）一个可学习的价值函数，将探索锚定在合理区域，从而减轻OOD风险，并实现可控外推以改进策略
- 实验：离线+在线，AIGB 出价赛道第一名

一些基础知识

自动出价问题

考虑在离散时间段 $i = 1, \cdots, I$ 内到达的一系列 $I$ 个曝光机会。广告商通过为这些曝光提交出价 $\{b_{i}\}_{i = 1}^{I}$ 参与实时竞争
拍卖机制遵循以下规则：
- 如果广告商的出价 $b_{i}$ 超过其他参与者的最高竞争出价 $b_{i}^{-}$，则该广告商赢得曝光 $i$
- 获胜的广告商随后会产生成本 $c_{i}$，该成本由拍卖机制确定，按照行业标准做法，论文采用 GSP 拍卖机制
广告商的目标 ：在指定时间段内通过赢得的曝光最大化总获取价值。这个优化问题可以正式表示为：
$$\max \sum_{i = 1}^{I} x_{i} v_{i}$$
- 其中 $v_{i} \in \mathbb{R}^{+}$ 表示广告商对曝光 $i$ 的私人估值（例如转化率或点击率），$x_{i} \in \{0, 1\}$ 表示指示拍卖结果的二元决策变量：
  $$x_{i}= \begin{cases}1 & \text{如果 } b_{i}>b_{i}^{-} \ 0 & \text{否则} \end{cases}$$
同时，广告商必须满足多个约束条件以确保有效的广告计划（campaign）管理。基本约束是总预算限制：
$$\sum_{i = 1}^{I} x_{i} c_{i} \leq B$$
- 其中 $B \in \mathbb{R}^{+}$ 表示广告商的总预算。其他关键绩效指标（KPI）约束，以每次获取成本（CPA）为例，可以表示如下：
  $$\frac{\sum_{i = 1}^{I} x_{i} c_{i} }{\sum_{i = 1}^{I} x_{i} v_{i} } \leq C \tag{4}$$
  - 其中 $C \in \mathbb{R}^{+}$ 表示最大允许的CPA。这个比率量化了广告支出相对于价值创造的效率。由于大多数其他KPI约束可以类似地建模，为简单起见，论文仅考虑CPA约束。然而，与由拍卖平台直接管理的预算约束不同，这些KPI约束在实际场景中通常并不严格。这是因为计算这些约束需要广告商对所有出价曝光的 $v_{i}$，因此只有在整个出价过程结束后才能确定真正的CPA。尽管如此，论文仍然希望在建模中将它们作为软约束使用
因此，整个出价过程可以表示为：
$$\begin{aligned} \max_{b_{1}, \cdots, b_{I} } & \sum_{i} x_{i} v_{i} \ \text{s.t.} & \sum_{i} x_{i} c_{i} \leq B \ & \frac{\sum_{i} x_{i} c_{i} }{\sum_{i} x_{i} v_{i} } \leq C \end{aligned} \tag{5}$$
解决这个优化问题存在固有的挑战，这源于曝光的高基数以及对未来拍卖表现的基本不确定性。先前的研究将这个问题重新表述为一个线性规划问题，以得出简化的最优出价策略：
$$b_{i}^{*}=\lambda_{0}^{*} v_{i}-\sum_{j} \lambda_{j}^{*}\left(q_{i j}\left(1-\mathbb{1}_{C R_{j} }\right)-\mathbb{k}_{j} \mathbb{p}_{i j}\right) \tag{6}$$
- 其中 $b_{i}^{*}$ 表示曝光 $i$ 的理论最优出价，$q_{ij}$ 可以是任何性能指标或常数，$\mathbb{1}_{C R_{1} }$ 是指示约束 $j$ 是否与成本相关的指标函数。$P_{i j}$ 和 $k_{j}$ 可以视为在多个KPI条件下公式（5）中 $v_{i}$ 和 $c$ 的扩展表达式。这种重新表述将自动出价问题转化为确定满足所有约束的最优 $\lambda_{0}^{*}$ 和 $\lambda_{j}^{*}$。通过将公式（6）代入公式（5），令 $j = 1$，$\mathbb{1}_{C R_{j} } = 1$，$\mathbb{P}_{i j} = v_{i}$，$k_{j} = C$ 且 $q_{i j}$ 为任何性能指标或常数，我们可以得到：
  $$b_{i}^{*}=\left(\lambda_{0}^{*}+\lambda_{1}^{*} C\right) v_{i}=\lambda^{*} v_{i} \tag{7}$$
  - 其中 $\lambda^{*}=\lambda_{0}^{*}+\lambda_{1}^{*} C$ 作为统一的出价参数。因此，许多近期研究试图通过在出价过程中迭代确定最优的 $\lambda^{*}$ 来解决出价问题。此外，值得注意的是，当根据公式（7）解决出价问题时，第一个条件，即 $\sum_{i} x_{i} c_{i} \leq B$ 总是满足的。这是因为当广告商的预算不足时，拍卖平台会自动控制 $x_{1}$，以确保广告商不欠款。然而，第二个条件并不总是满足，因为论文预测的 $\lambda$ 与最优的 $\lambda^{*}$ 之间存在差距。解决这个问题的一个简单方法是在评估阶段为模型选择在公式（7）的目标函数中添加一个关于CPA条件的惩罚项，这将在3.2节中进一步讨论

基于 DT 的自动出价

为解决自动出价问题，现有方法采用基于规则的策略或RL方法进行优化。然而，基于规则的策略通常无法适应现实出价环境的高度动态性，而RL方法依赖于由 $s_{t + 1} = f(s_{t}, a_{t})$ 定义的状态转换，这使得对拍卖生态系统中固有的重要时间依赖关系和历史观测进行建模变得复杂
Transformer架构的最新进展催生了 DT，使其成为顺序决策的最先进方法。DT 在捕捉长程依赖关系方面表现出色，使其非常适合拍卖结果显示出显著时间相关性的出价环境。基于这个框架，论文将自动出价视为 DT 设置下的序列建模任务。出价期被划分为离散的时间步，每个时间步在特定的环境设置下进行配置：
- 状态 $s_{t}$ ：状态向量 $s_{t}$ 包含一系列特征，用于描述时间步 $t$ 的出价条件。对于广告场景，这些特征可以是剩余时间、未使用的预算、历史出价统计信息等
- 动作 $a_{t}$ ：动作 $a_{t}$ 表示在整个出价期内可以迭代调整的出价变量。在论文中，根据公式（7），最优动作是 $a = \lambda^{*}$。因此，论文将时间步 $t$ 的实际动作表示为： $a_{t}=\lambda_{t}$
- 奖励 $rw_{t}$ ：假设有 $N_{t}$ 个候选曝光在时间步 $t$ 到 $t + 1$ 之间到达。奖励 $rw_{t}$ 可以定义为： $rw_{t}=\sum_{n = 0}^{N_{t} } x_{n_{t} } v_{n_{t} }$，其中 $x_{n_{t} }$ 和 $v_{n_{t} }$ 是时间步 $t$ 第 $n$ 个曝光的二元指示符和价值
- 未来回报（Return-To-Go, RTG） $r_{s}$ ： RTG 值表示在未来时间步中要获得的总奖励： $r_{t}=\sum_{t’ = t}^{T} rw_{t’}$，其中 $T$ 是最后一个时间步
这些设置导致了以下轨迹表示，非常适合自回归训练和推理：
$$\tau=\left(r_{1}, s_{1}, a_{1}, r_{2}, s_{2}, a_{2}, \cdots, r_{T}, s_{T}, a_{T}\right)$$

GAVE 整体框架介绍

GAVE概述

GAVE整体架构：
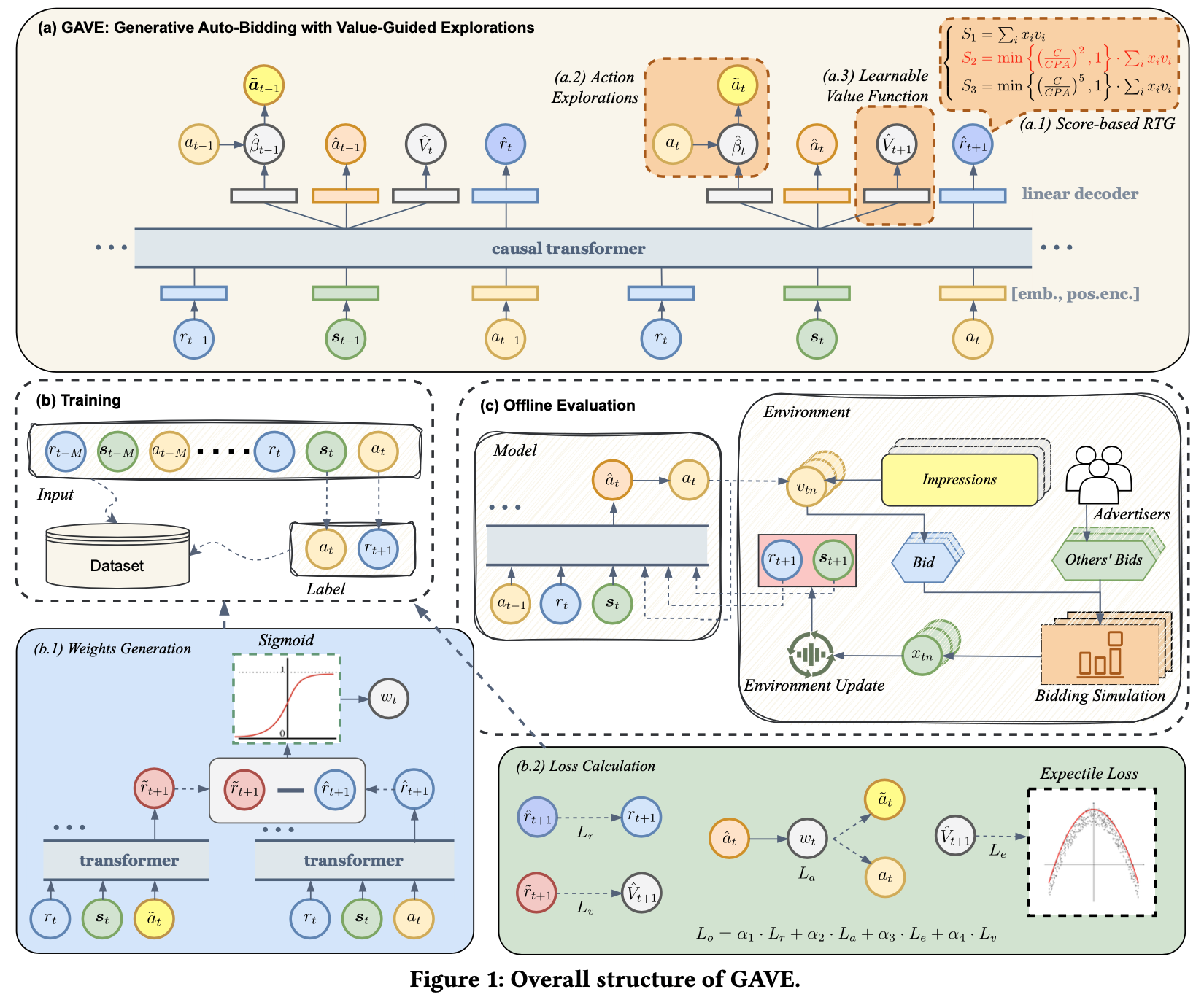
如图1所示，GAVE采用 DT 架构，其中 RTG、状态和动作对构成输入序列，即时间戳 $t$ 处的 $(r_{t}, s_{t}, a_{t})$。与传统 DT 不同，GAVE引入了几个关键创新，以实现自适应优化、增强稳定性并促进策略改进，这些创新包括
- 自适应的 RTG ：用于与多样化广告目标对齐的 Score-based RTG （图1（a.1））
- 配备基于 RTG 评估机制的动作探索模块（图1（a.2）），用于发现和评估新动作并稳定更新
- 一个可学习的价值函数（图1（a.3）），用于引导探索以改进策略 ，同时减轻分布外（OOD）风险。GAVE的训练遵循离线范式（图1（b）），使用序列样本作为输入生成预测标签
- 为进行评估，采用模拟出价环境（图1（c）），其中测试模型与固定策略智能体进行交互
GAVE的预测过程如下所示：
$$\left\{\begin{array}{l} \left(\hat{\beta}_{t}, \hat{a}_{t}, \hat{V}_{t+1}\right)=GAVE(r_{t-M},s_{t-M},a_{t-M},\cdots ,r_{t},s_{t})\\ \hat {r}_{t+1}=GAVE(r_{t-M},s_{t-M},a_{t-M},\cdots ,r_{t},s_{t},a_{t})\\ \tilde {a}_{t}=\hat {\beta }_{t}a_{t}\end{array} \right.$$
- 其中 $M$ 是一个超参数，表示具有 $M + 1$ 个输入时间步的序列
GAVE采用自适应的 Score-based RTG 函数 ，可以使优化目标与不同的广告目标保持一致：在时间步 $t$ 的动作探索过程中，除了预测动作 $\hat{a}_{t}$ 之外，GAVE还预测以下内容：
- 一个系数 $\hat{\beta}_{t}$
  - 问题：$\hat{\beta}_{t}$ 的训练依赖 $\tilde {a}_{t}$，继而依赖 $\tilde {r}_{t}$，损失函数见文章后面的公式（22）？是否在图1（a.2）中还需要接一个网络预估 $\tilde{r}_{t}$ 才能反传损失函数吗？
  - 回答：从源码看，是的，且使用的是和主网络相同的同一个 transformer 网络
    - transformer 网络过程见：CAVE/…/dt.py：$\tilde {a}_{t}\rightarrow \tilde {r}_{t}$ 定义
    - 损失函数见：CAVE/…/dt.py：$L_v$ 定义
- 一个用于估计可学习价值函数 $V_{t + 1}$ 的 $\hat{V}_{t + 1}$（注：文章后面会介绍，损失函数是分位点回归）
- 一个 RTG 值 $\hat{r}_{t + 1}$ （注：文章后面会介绍，拟合目标是真实的 RTG $r_{t+1}$）
以下创新共同使GAVE能够实现更好的性能和鲁棒性：
- 通过使用基于 RTG 的评估方法评估探索动作 $\tilde{a}_{t}$ 和动作标签 $a_{t}$，GAVE应用平衡更新策略来协调 $\tilde{a}_{t}$ 和 $a_{t}$。这确保了一个保持稳定性的更新过程
- 引入可学习的价值函数 $V_{t + 1}$ 来引导模型朝着潜在的最优策略改进，同时进一步降低OOD风险

Score-based RTG

如2.1节所述，直接优化赢得曝光的累积价值可能会导致每次行动成本（CPA）约束显著超出其限制范围。为解决这个问题，可以构建包含惩罚项的目标函数作为评估指标，从而能够依据特定的广告目标调整对CPA限制的重视程度
- 这种方式有助于对最优模型进行评估和筛选。例如，先前的研究工作[44]提出在测试阶段使用分数 $S$ 来评估模型的实际性能，进而能够挑选出性能更优的模型。该分数整合了针对CPA约束的惩罚项，用于评估整个出价周期内出价模型的整体表现，公式如下：
  $$\begin{cases}
  CPA = \frac{\sum_{i} x_{i} c_{i} }{\sum_{i} x_{i} v_{i} } \\
  \mathbb{P}(CPA; C) = \min\left\{\left(\frac{C}{CPA}\right)^{\gamma}, 1\right\} \\
  S = \mathbb{P}(CPA; C) \cdot \sum_{i} x_{i} v_{i}
  \end{cases} \tag{13}$$
- 注：前文已经定义过，$C$ 是允许的最大 $CPA$
- 理解： $CPA > C$ 时，$\mathbb{P}(CPA; C) < 1$ 成立，此时原始收益会变小
在论文中，论文将约束条件直接融入训练阶段，不再仅仅依赖于预训练模型的选择来提升评估分数（如何理解？）
- 为了使训练与各种广告目标的评估指标保持一致，论文提出在 GAVE 中采用带约束的分数函数（而非无约束的 $\sum_{i = 1}^{I} x_{i} v_{i}$）来进行 RTG 建模，如图1（a.1）所示。例如，基于公式（13）所定义的评估指标，可以利用以下 Score-based RTG 函数来使训练与评估同步：
  $$\begin{cases}
  CPA_{t} = \frac{\sum_{i}^{I_{t} } x_{i} c_{i} }{\sum_{i}^{I_{t} } x_{i} v_{i} } \\
  \mathbb{P}(CPA_{t}; C) = \min\left\{\left(\frac{C}{CPA_{t} }\right)^{\gamma}, 1\right\} \\
  S_{t} = \mathbb{P}(CPA_{t}; C) \cdot \sum_{i}^{I_{t} } x_{i} v_{i} \\
  r_{t} = S_{T} - S_{t - 1}
  \end{cases} \tag{14}$$
- $I_{t}$ 表示从时间步0到时间步 $t$ 的曝光数量
- $S_{t}$ 代表时间步 $t$ 的广义分数函数
- $T$ 表示出价周期中的最后一个时间步
- 通过将分数计算推广到每个时间步，推导出 RTG $r_{t}$，以表示尚未获得的未来分数，进而引导GAVE的优化方向
此外，在实际应用中，不同的广告目标对CPA约束的依赖程度可能有所不同，从而产生不同的评估指标。尽管如此，通过以类似的方式将分数推广到每个时间步（即 $S_{t}$），训练和评估仍可保持一致，公式如下：
$$r_{t} = S_{T} - S_{t - 1} \tag{15}$$
这种 Score-based RTG 函数增强了 GAVE 的灵活性，确保其能够适用于各种不同的广告目标
问题：在推理阶段，广告曝光次数等是未知的，如何设计对应的 RTG？

Action Explorations

本节的主要目标是在训练过程中探索新的动作，以发现离线数据集中可能缺失的策略，从而实现更好的模型优化，但离线环境动作探索面临以下问题：
- 不探索面临的问题 ：在离线环境中，由于无法与环境进行交互，仅从固定的数据集中学习可能会导致模型局限于已记录的行为模式
- 探索面临的问题 ：但在数据集之外探索动作可能会引入固有的分布转移，进而可能导致行为崩溃[6, 21]（与实际动作标签相比，探索出的动作对模型性能的影响可能是有益的，也可能是有害的，这给开发保持稳定性的更新过程带来了巨大挑战）
为应对这些挑战，GAVE 引入了一种全新的动作探索机制，并结合基于 RTG 的评估方法，如图1（a.2）所示。这使得GAVE能够通过识别动作的重要性，自适应地调整动作的探索和更新方向，从而实现保持稳定性的更新
- 具体而言，在时间步 $t$，GAVE预测一个与 $a_{t}$ 维度相同的系数 $\hat{\beta}_{t}$，以生成一个新的动作 $\tilde{a}_{t}$。该过程的正式表达式为：
  $$\begin{cases}
  \hat{\beta}_{t} = \sigma(FC_{\beta}( DT (r_{t - M}, s_{t - M}, a_{t - M}, \cdots, r_{t}, s_{t}))) \\
  \tilde{a}_{t} = \hat{\beta}_{t}a_{t}
  \end{cases}$$
  - 如前文所述，$M$ 是一个超参数，表示具有 $M + 1$ 个输入时间步的序列
其中，$ DT (\cdot)$ 表示 DT backbone（主干网络），$FC_{\beta}(\cdot)$ 表示全连接层，$\sigma$ 是缩放函数。为减轻分布外（OOD）问题，缩放函数定义为：
$$\sigma(x) = Sigmoid(x) + 0.5$$
- 该公式将 $\hat{\beta}_{i}$ 限制在区间 $[0.5, 1.5]$ 内，确保探索出的动作 $\tilde{a}_{t}$ 与动作标签 $a_{t}$ 保持接近
为了在训练过程中最小化分布转移并实现保持稳定性的更新，论文并未直接使用 $\tilde{a}_{t}$ 来生成新样本，而是将其作为额外标签，与原始标签 $a_{t}$ 共同平衡动作更新
- 这种方法需要估计 $\tilde{a}_{t}$ 和 $a_{t}$ 的相对重要性，以确定预测动作 $\hat{a}_{t}$ 的最优更新方向
- 根据强化学习的惯例[21, 39, 41]，论文将 $a_{t}$ 的动作价值定义为 $r_{t + 1}$ （时间步 $t + 1$ 的 RTG），因为它 代表了执行动作 $a_{t}$ 后 未来的累积回报
论文设计了如图1（b.1）所示的 $w_{t}$，以平衡更新方向：
$$\begin{cases}
\tilde{r}_{t + 1} = GAVE(r_{t - M}, s_{t - M}, a_{t - M}, \cdots, r_{t}, s_{t}, \tilde{a}_{t}) \\
\hat{r}_{t + 1} = GAVE(r_{t - M}, s_{t - M}, a_{t - M}, \cdots, r_{t}, s_{t}, a_{t}) \\
w_{t} = Sigmoid(\alpha_{r} \cdot (\tilde{r}_{t + 1} - \hat{r}_{t + 1}))
\end{cases} \tag{18}$$
- 其中，$\tilde{r}_{t + 1}$ 和 $\hat{r}_{t + 1}$ 分别表示 $\tilde{a}_{t}$ 和 $a_{t}$ 的估计 RTG
- 问题：$\alpha_{r}$ 是超参数吗？如何设置？
- 相应的动作探索损失函数定义为：
  $$\begin{cases}
  L_{r} = \frac{1}{M + 1} \sum_{t - M}^{t}(\hat{r}_{t + 1} - r_{t + 1})^{2} \\
  L_{a} = \frac{1}{M + 1} \sum_{t - M}^{t}((1 - w_{t}’) \cdot (\hat{a}_{t} - a_{t})^{2} + w_{t}’ \cdot (\hat{a}_{t} - \tilde{a}_{t}’)^{2})
  \end{cases} \tag{19}$$
  - $w’$ 和 $\tilde{a}_{t}’$ 表示梯度冻结后的 $w$ 和 $\tilde{a}_{t}$
  - $\hat{a}_t$ 是预测动作，也是 $L_{a}$ 的学习目标
  - 通过 $L_{r}$，GAVE 确保了 RTG 预测的准确性，能够可靠地估计 $\tilde{a}_{t}$ 和 $a_{t}$ 的 RTG
  - 通过 $L_{a}$，GAVE 在 $\tilde{a}_{t}$ 和 $a_{t}$ 之间维持了平衡且保持稳定性的更新过程，当 $w_{t} > 0.5$ 时，更新方向朝着 $\tilde{a}_{t}$ ；否则，朝着 $a_{t}$，以此减轻OOD问题以及探索可能带来的负面影响
    - 理解：当 $w_{t} > 0.5$ 时，说明探索动作 $\tilde{a}_{t}$ 预估的 RTG $\tilde{r}_{t + 1}$ 比真实动作 $a_{t}$ 预估的 RTG $\hat{r}_{t + 1}$ 好的比较多，值得让 $\hat{a}_t$ 朝探索动作 $\tilde{a}_{t}$ 更新一些

Learnable Value Function

虽然动作探索机制确保了在数据集之外进行探索并实现保持稳定性的更新过程，但随机生成的 $\tilde{a}_{t}$ 并不能保证提升模型性能。为解决这一局限性，论文提出了一种可学习价值函数，如图1（a.3）所示，该函数有助于发现更优的动作以改进策略。具体而言，受强化学习惯例[21, 39, 41]的启发，论文提出了一个序列价值函数 $V_{t + 1}$，类似于强化学习中的最优状态价值函数，它表示 $r_{t + 1}$ 的上限，公式如下：
$$V_{t + 1} = \underset{a_{t} \in \mathbb{A} }{\arg \max} \ r_{t + 1} \tag{20}$$
- $\mathbb{A}$ 表示可用动作空间
- 由于动作空间广泛，且离线数据集中的实际动作有限，直接对 $V_{t + 1}$ 进行统计计算并不可行。论文使用 $r_{t + 1}$ 的期望分位数回归过程来学习这个值：
  $$\begin{align}
  L_{e} &= \frac{1}{M + 1} \sum_{t - M}^{t}(L_{2}^{\tau}(r_{t + 1} - \hat{V}_{t + 1})) \\
  &= \frac{1}{M + 1} \sum_{t - M}^{t}(\left|\tau - \mathbb{1}((r_{t + 1} - \hat{V}_{t + 1}) < 0)\right|(r_{t + 1} - \hat{V}_{t + 1})^{2})
  \end{align} \tag{21}$$
  - $\hat{V}_{t + 1}$ 表示 $V_{t + 1}$ 的预测值
  - $L_{2}^{\tau}(y - m(x))$ 表示使用模型 $m(x)$ 预测标签 $y$ 的期望分位数 $\tau \in (0, 1)$ 时的损失函数[21]。根据公式（20），论文将 $\tau = 0.99$，以学习 $r_{t + 1}$ 的上限，从而有效地估计 $V_{t + 1}$
通过使用 $\hat{V}_{t + 1}$ 估计 $V_{t + 1}$，并利用它来指导 $\tilde{r}_{t + 1}$ 的更新方向，GAVE隐式地将探索出的 $\tilde{a}_{t}$ 的更新方向引导向潜在的最优动作。这一过程如图1（b.2）所示，可正式表示为：
$$L_{v} = \frac{1}{M + 1} \sum_{t - M}^{t}(\tilde{r}_{t + 1} - \hat{V}_{t + 1}’)^{2} \tag{22}$$
- 其中，$\hat{V}_{t + 1}’$ 表示梯度冻结后的 $\hat{V}_{t + 1}$。通过应用 $L_{v}$，GAVE将 $\tilde{a}_{t}$ 的 RTG 锚定在 $\hat{V}_{t + 1}$ 附近，从而隐式地将 $\tilde{a}_{t}$ 的更新方向引导向最优动作。这种方法减轻了OOD风险，并实现了可控的外推以改进策略

Optimization Algorithm

通过上述机制，GAVE实现了一个离线生成式自动出价框架，该框架结合了价值引导的探索，以增强策略学习能力。综合损失函数由公式（19）、（21）和（22）中定义的各个组件加权组合而成：
$$L_{o} = \alpha_{1} \cdot L_{r} + \alpha_{2} \cdot L_{a} + \alpha_{3} \cdot L_{e} + \alpha_{4} \cdot L_{v} \tag{23}$$
- 其中，${\alpha_{1}, \alpha_{2}, \alpha_{3}, \alpha_{4} }$ 是超参数，用于控制每个损失组件的相对贡献
GAVE的完整优化过程在算法1中详细列出，训练过程如图1（b）所示
在推理过程中，如图1（c）所示，GAVE处理每个输入序列以预测 $\hat{a}_{t} = \lambda_{t}$，它作为时间步 $t$ 的出价参数。然后，根据公式（7），时间步 $t$ 第 $n$ 个曝光的出价计算为 $b_{t n} = \lambda_{t} v_{t n}$，从而实现实时出价模拟

离线实验

在本节中，论文在两个公共数据集上进行实验，以研究以下问题：
- RQ1 ：与最先进的自动出价基线方法相比，GAVE 的性能如何？
- RQ2 ：GAVE 能否适应多样化的广告目标？
- RQ3 ：可学习价值函数在促进动作探索方面的效果如何？
- RQ4 ：GAVE 中所提出的组件对最终出价性能有何贡献？

Experiment Setup

数据集 ：先前的自动出价研究主要依赖于专有出价日志进行评估，问题的表述往往针对特定场景。这种评估方法的异质性阻碍了不同方法之间进行公平、系统的比较。最近，阿里巴巴妈妈推出了AuctionNet，这是行业内首个标准化的大规模模拟出价基准，能够在一致的条件下对模型进行全面评估。在本研究中，论文使用AuctionNet框架中的两个数据集：
- （i）AuctionNet：主要数据集，包含全面的出价轨迹；
- （ii）AuctionNet-Sparse：AuctionNet的稀疏变体，具有较低的转化率
- 以上这两个数据集都包含约 50 万个出价轨迹，收集自 1 万个不同的投放期，每个投放期由 48 个时间步组成，并且包含来自数百万个曝光机会的交互数据。详细统计信息见表1
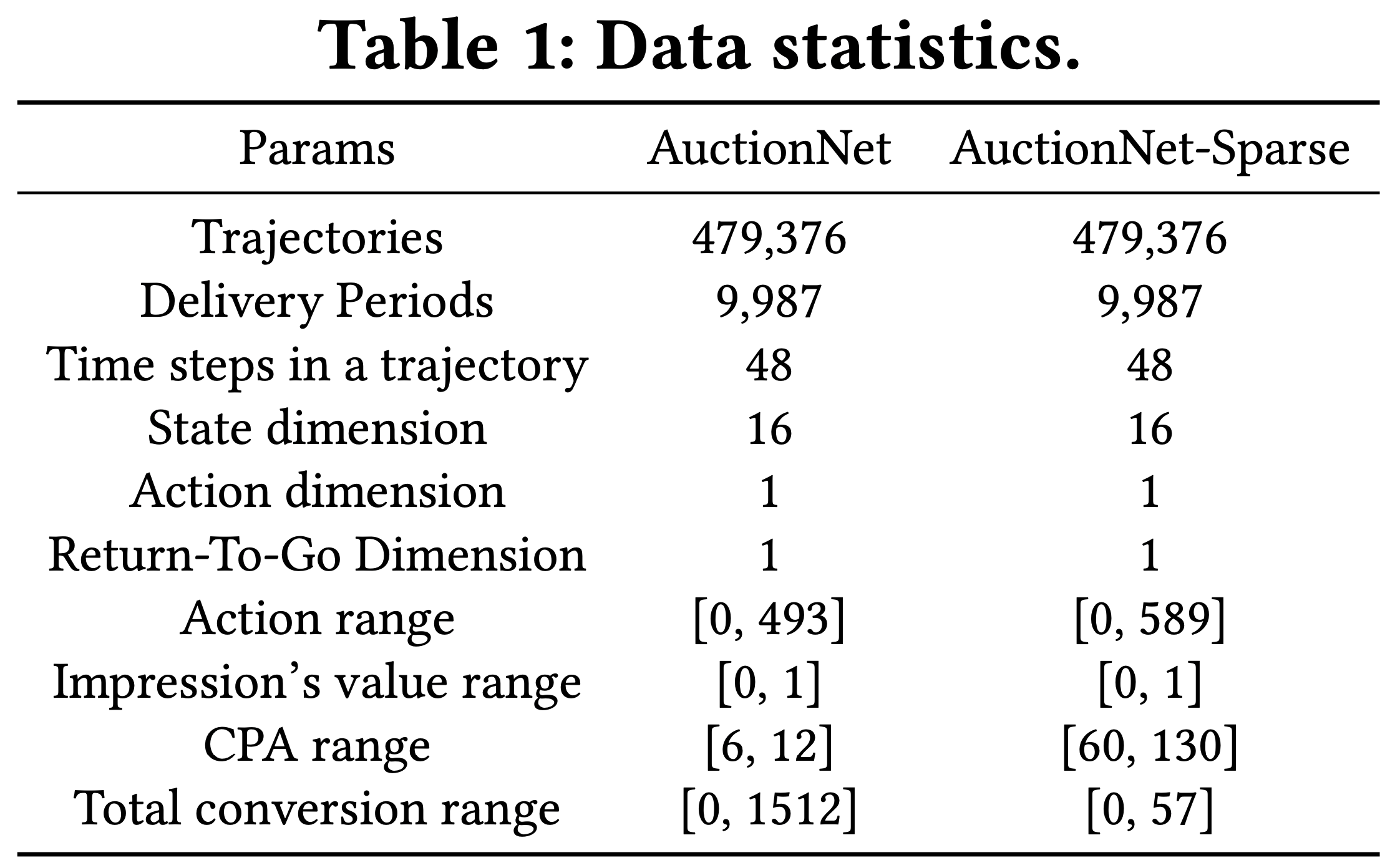
评估协议 ：论文的评估方法遵循AuctionNet基准，并采用模拟环境来模拟现实世界的广告系统，如图1（c）所示
- 评估涵盖一个 24 小时的投放期，离散化为 48 个均匀的时间步，在此期间，预测动作用于出价（$(\hat{a}_{t} = a_{t})$）
- 在这个模拟环境中，48个具有不同策略的出价智能体竞争即将到来的（incoming）曝光机会，性能使用公式（13）（$\gamma = 2$）进行衡量。为确保全面评估，论文采用循环测试策略：测试模型依次替换48个智能体中的每一个，在每一轮中与其余智能体竞争。最终性能计算为所有评估的平均得分，从而提供了对模型有效性的可靠衡量
基线方法 ：为评估GAVE的有效性，论文将其与多种基线方法进行全面比较：
- DiffBid：应用扩散框架来模拟出价轨迹并对出价序列进行建模
- USCB：在在线RL出价环境中动态调整出价参数以实现最优出价性能
- CQL：学习一个保守的价值函数，以减轻 Offline RL 中的高估问题
- IQL：应用期望分位数回归方法，在不评估超出范围动作的情况下实现策略改进
- BCQ：在典型的 Offline RL 学习过程中对动作空间施加限制
- DT：采用transformer架构进行顺序决策建模，并使用行为克隆方法从数据集中学习平均策略
- CDT：尝试在离线设置中训练一个约束满足策略，以平衡安全性和任务性能
- GAS：尝试通过在建模中应用蒙特卡洛树搜索（MCTS）来构建一个基于 DT 的离线出价框架，并进行训练后搜索
实现细节 ：根据先前的研究，论文使用原始数据集中不同的预算比率进行评估。性能使用以下评分指标衡量：
$$S = \mathbb{P}(CPA; C) \cdot \sum_{i} x_{i} v_{i}$$
该指标如公式（13）所定义，其中 $Y = 2$。所有实验均在NVIDIA H100 GPU上进行，使用固定的批量大小128，最大训练步数为40万步。GAVE的实现采用具有8层和16个注意力头的因果transformer架构。模型参数使用AdamW优化器进行优化，学习率为 $1e^{-5}$。其他超参数通过全面的网格搜索确定，以最大化性能。为确保统计显著性，论文使用最优参数配置进行10次独立运行，并报告平均性能指标

整体性能（RQ1）

论文在不同预算设置下对GAVE和各种基线方法进行了全面比较，结果汇总在表2中
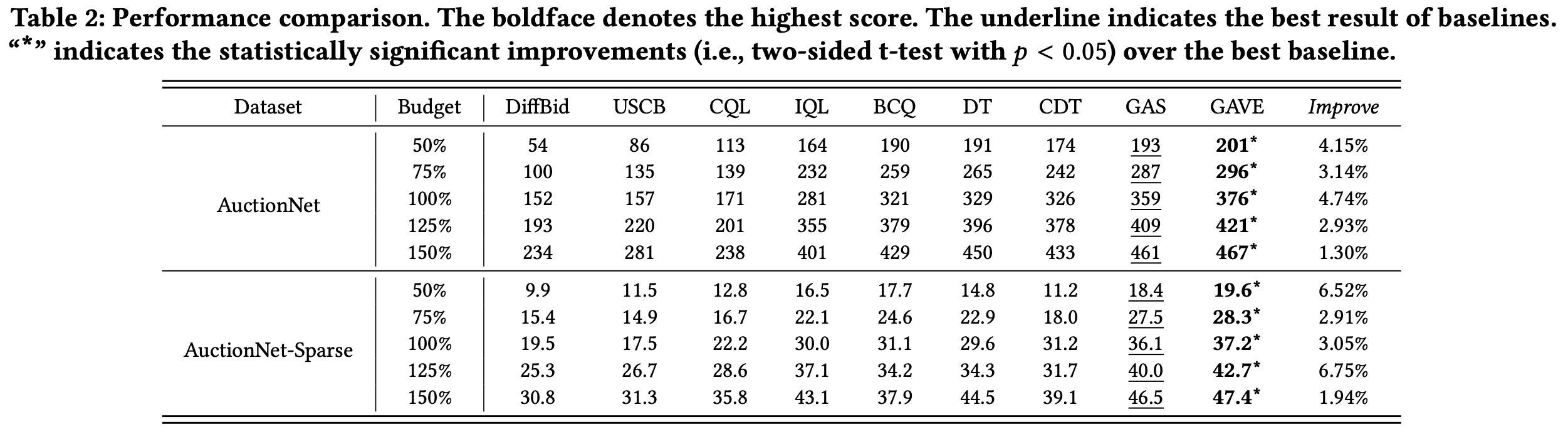
实验分析揭示了几个关键发现：
- GAVE在所有预算和数据集配置下均表现出色，始终优于现有方法。这种优越性可归因于论文新颖的动作探索方法，该方法在价值函数的指导下，能够在离线数据集之外发现新颖的、潜在的最优动作，同时通过平衡探索收益和风险的稳定更新过程保持稳健的训练
- 在所有基线方法中，基于 DT 的方法（GAS、 DT 和 CDT）表现较为突出，这凸显了 DT 结构在捕捉时间依赖关系和促进出价场景中的顺序决策方面的有效性。值得注意的是，GAS比 DT 和 CDT 取得了更好的结果，验证了其MCTS实现对策略优化的有效性。DiffBid在数据集上的表现不佳，可能是由于长序列和高度动态的环境给DiffBid准确预测轨迹和从反向过程中学习带来了额外挑战

一致性分析（RQ2）

如3.2节所述，广告目标可能需要不同的评估指标。为解决这一问题，GAVE采用了 Score-based自适应 RTG 建模方法，该方法能够适应各种优化目标，从而使训练目标与评估指标保持一致，如公式（15）所示。在本节中，论文探究GAVE在不同 RTG 和评估指标配置下的性能，以回答RQ2。具体而言，论文考虑以下三种评估指标：
$$\begin{cases}
S_{1}=\sum_{i} x_{i} v_{i} \\
S_{2}=\min\left\{\left(\frac{C}{CPA}\right)^{2}, 1\right\} \cdot \sum_{i} x_{i} v_{i} \\
S_{3}=\min\left\{\left(\frac{C}{CPA}\right)^{5}, 1\right\} \cdot \sum_{i} x_{i} v_{i}
\end{cases}$$
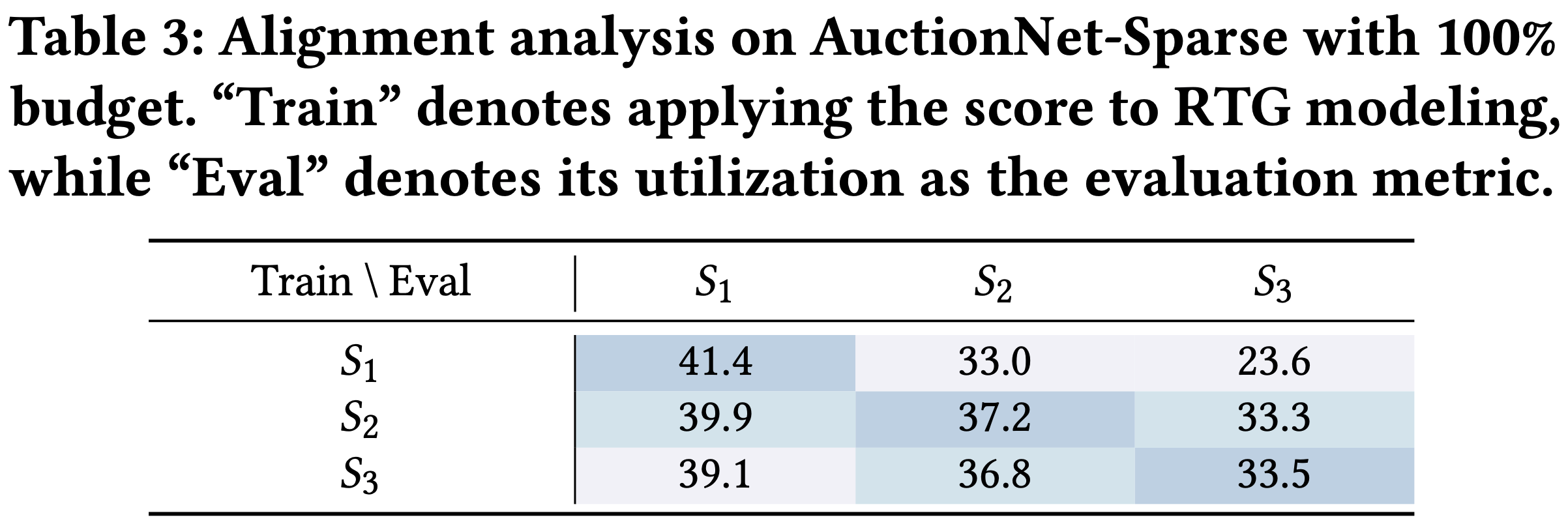
- 其中，$S_{1}$ 仅考虑获得的总曝光价值，代表对CPA条件限制较为宽松的业务场景。$S_{2}$ 是论文的优化目标和评估分数，它对CPA约束添加了惩罚项。$S_{3}$ 进一步提高了CPA的惩罚系数，代表对CPA条件限制严格的业务场景。这些指标既可以在训练期间用于 RTG 建模，也可以在测试期间用作评估标准。结果如表3所示
从表3中可以观察到，当训练 RTG 与用作评估指标的函数一致时，GAVE始终能取得最高性能。这一发现强调了通过论文 Score-based RTG 方法使训练目标与特定评估指标保持一致的重要性
注：表3体现不出来自适应能力吧，毕竟没有对照，靠衰减不多来说明目标变化时的有效性吗？

参数分析（RQ3）

为回答RQ3，论文对权重 $w_{t}$ 进行参数分析，如图1（b.1）所示，以阐明训练过程中 $\tilde{a}_{t}$ 和 $a_{t}$ 之间的差异。具体而言，图2曝光了训练步骤中平均总损失 $L_{o}$ 和权重 $w_{t}$ 的变化情况，使论文能够监测 $\tilde{r}_{t + 1}$ 和 $\hat{r}_{t + 1}$ 之间的差异。$w_{t}$ 越大，表明 $\tilde{r}_{t + 1}$ 对 $\hat{r}_{t + 1}$ 的影响越大，进而证明 $\tilde{a}_{t}$ 优于 $a_{t}$。这一结果凸显了价值函数在指导动作探索方面的有效性
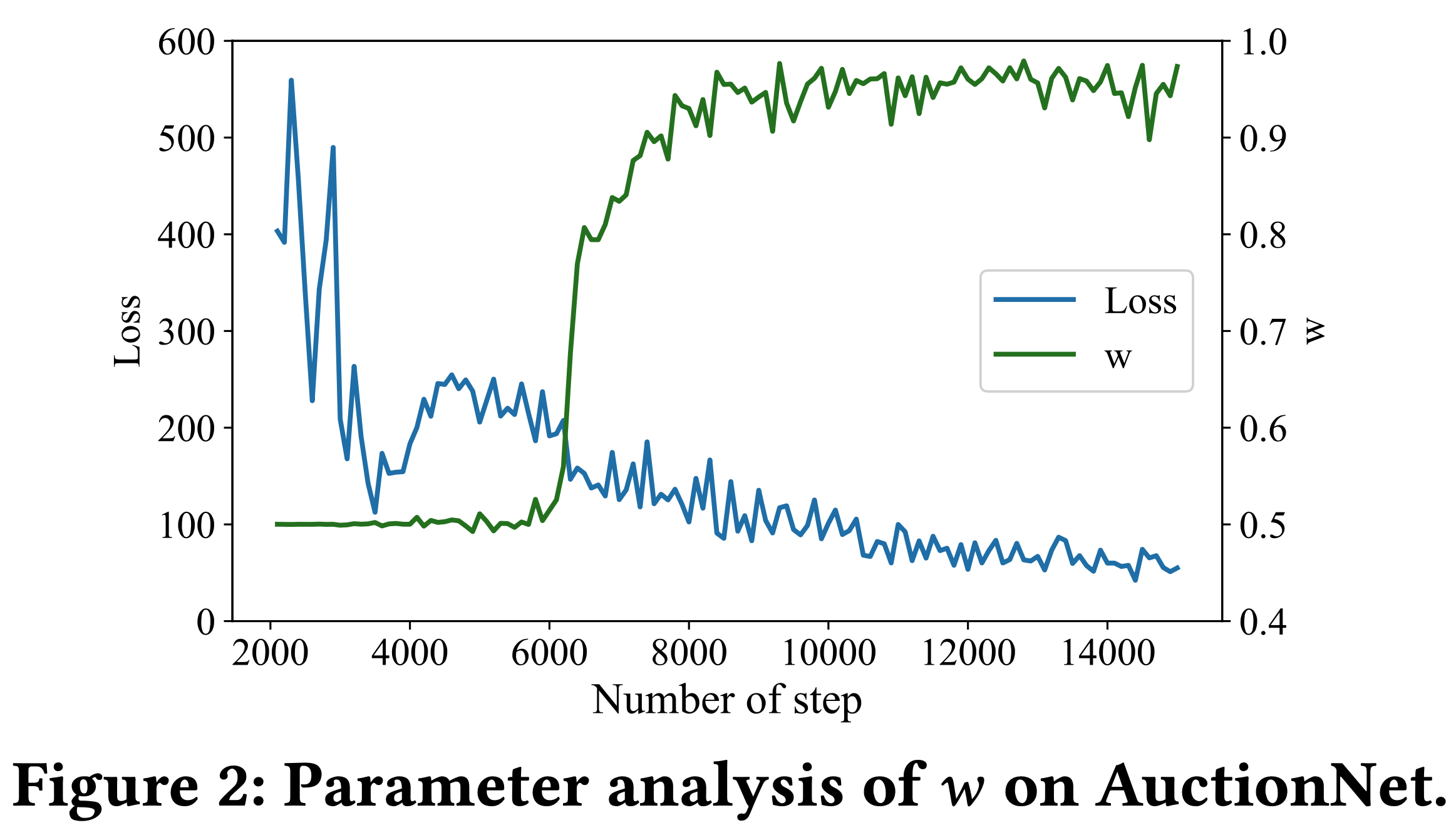
从图2中明显可以看出，随着训练的进行，参数 $w_{t}$ 从约0.5增加到稳定高于0.5的位置。该稳定位置受数据集分布和模型超参数的共同影响。这一趋势证实了可学习价值函数在指导动作探索方面的有效性。在价值函数的引导下，模型持续探索具有更高 RTG 值 $\tilde{r}_{t + 1}$ 且接近估计最优值 $\hat{V}_{t + 1}$ 的动作 $\tilde{a}_{t}$。这种方法有助于学习潜在的最优策略，同时减轻OOD问题

消融研究（RQ4）

为进一步阐明GAVE中每个模块的贡献以回答RQ4，论文进行了消融研究，评估以下修改版本的GAVE：
GAVE-V ：不包含3.4节中描述的可学习价值函数。在此配置下，损失函数 $L_{v}$ 和 $L_{e}$ 被以下更新规则取代，以确保探索出的动作通过提高其 RTG 值 $\tilde{r}_{t + 1}$ 总体上优于原始标签：
$$L_{w}=1 - Sigmoid\left(\alpha_{r} \cdot \left(\tilde{r}_{t + 1}-\hat{r}_{t + 1}’\right)\right)$$
- 其中，$\hat{r}_{t + 1}’$ 是 $\hat{r}_{t + 1}$ 的梯度冻结版本。然而，由于没有价值函数，$\tilde{r}_{t + 1}$ 的更新方向变得无界，导致OOD问题和次优性能
GAVE-VA ：既不包含3.4节中的价值函数，也不包含3.3节中详细介绍的动作探索机制
DT ：移除所有与GAVE相关的设计模块，包括3.4节、3.3节和3.2节中描述的模块。因此，此配置与纯 DT 框架一致，使用 $S=\sum_{i} x_{i} v_{i}$ 进行 RTG 建模
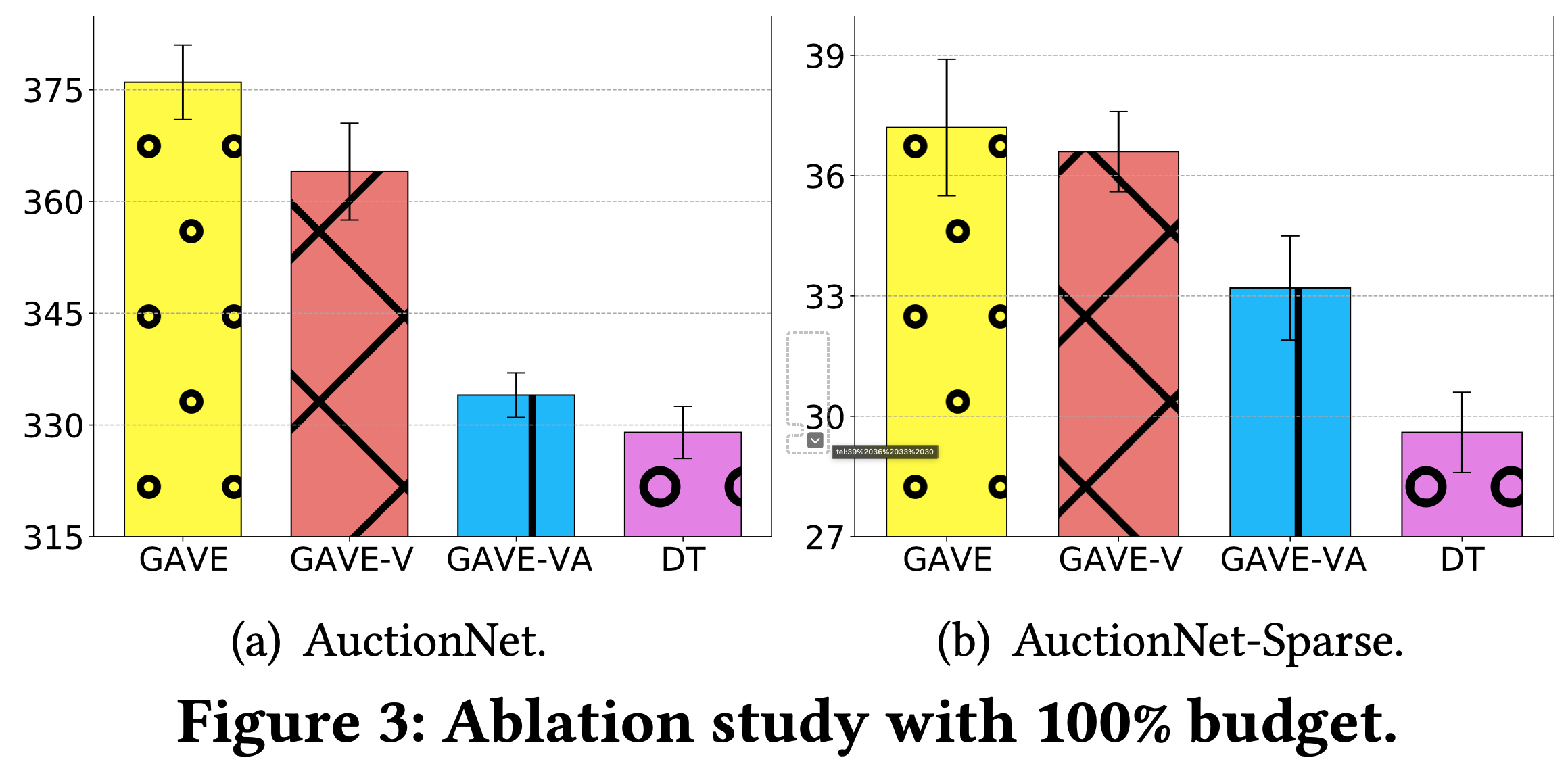
图3曝光了评估结果。结果表明：
- （i）使用 Score-based RTG 建模使优化目标与评估指标保持一致，这使得GAVE-VA的性能优于 DT，证明了训练中目标一致性的重要性；
- （ii）GAVE-V中融入动作探索机制和基于 RTG 的评估，使模型能够发现离线数据集之外的潜在策略，并评估其重要性以实现稳定更新过程，从而比GAVE-VA取得更好的性能；
- （iii）GAVE中完全集成价值函数以指导动作探索，利用了潜在的最优策略，进一步缓解了OOD问题并提高了整体性能

在线部署

论文通过在两个工业实时出价场景（Nobid 和 Costcap）中的A/B测试来评估GAVE的有效性。Nobid 旨在在每日预算内最大化转化次数，Costcap 旨在在CPA/ROI限制下最大化转化次数。实验设置如下：
- 状态：20步的序列，特征包括预算、CPA限制、预测值、流量/成本速度、时间分段预算、剩余时间和窗口平均出价系数
- 动作：为稳定出价结果，出价系数 $\lambda$ 基于前两小时包含 $E$ 个时间步的窗口平均值确定，$\lambda_{t}=a_{t}+\frac{1}{|E|} \sum_{t’=t-E}^{t-1} \lambda_{t’}$，其中 $a_{t}$ 是GAVE在时间步 $t$ 的输出动作
- 未来回报（RTG） ：鉴于实际转化的稀疏性，论文在训练期间使用预期总转化次数 $\sum_{i} pcvr_{i}$，其中 $pcvr_{i}$ 是赢得流量 $i$ 的预测转化率。在推理时，整个序列的 RTG 设置为前一天广告计划的总预期转化次数
论文将GAVE与目前正在实际应用中的离线强化学习算法IQL进行比较
- 评估指标包括成本、转化次数、目标成本和CPA有效率，出价策略侧重于在预算和CPA约束下最大化转化次数
- 为考虑不同的广告计划目标，目标成本作为一种价值加权的转化度量，对于 Costcap 广告计划，转化价值等于CPA限制；对于 Nobid 广告计划，使用总流量的平均实际 CPA
- 如果 Costcap 广告计划的 CPA 保持在限制以下，则认为其 CPA 有效，该指标仅针对 Costcap 广告计划进行评估。论文进行了为期五天的在线A/B测试，将每个广告计划25%的预算和流量分配给基线出价模型和GAVE，结果汇总在表4中
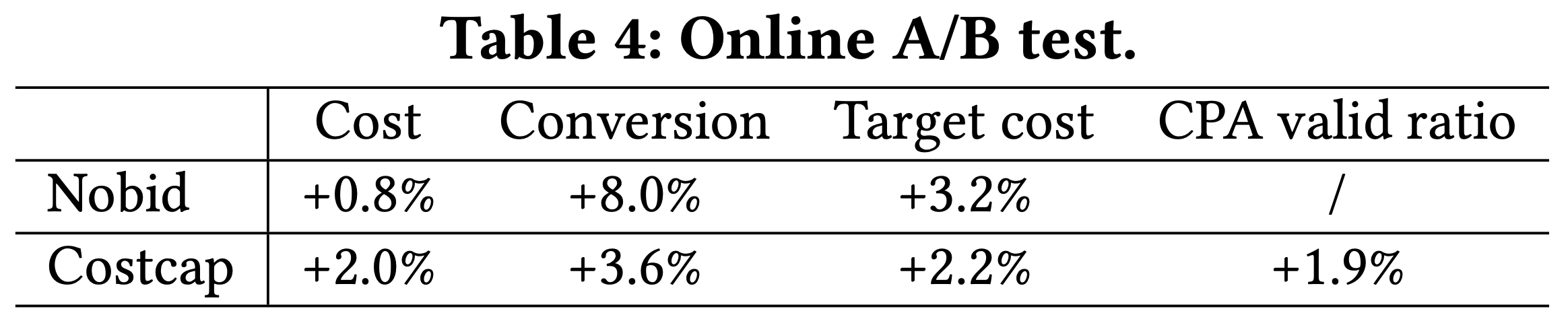
对于 Nobid 和 Costcap 广告计划，GAVE均改善了成本和转化次数指标。在 Nobid 广告计划中，GAVE使成本增加了0.8%，转化次数增加了8.0%，目标成本增加了3.2%。在 Costcap 广告计划中，广告收入和广告商价值有所提升，同时CPA有效性显著改善，成本增加2.0%，转化次数增加3.6%，目标成本增加2.2%，有效CPA率增加1.9%

结论

论文提出了GAVE，通过价值引导探索来增强 DT 在离线生成式自动出价中的应用
- 为适应复杂的广告目标，论文设计了一种可定制的 Score-based RTG 机制，能够对各种优化目标进行自适应建模，以匹配不同的评估指标
- 论文将动作探索机制与基于 RTG 的评估方法相结合，在离线数据集之外探索动作的同时，确保稳定的更新过程
- 为进一步引导探索并减轻 OOD 风险，论文采用了可学习价值函数，将 RTG 更新锚定在分布合理的区域，同时允许可控的外推以改进策略
大量实验、在线部署和 NeurIPS 竞赛结果表明，论文的 GAVE 框架在增强自动出价策略的适应性和性能方面是有效的，为在动态环境中优化数字广告计划提供了一种通用解决方案

CA——GAVE

整体思路

一些讨论

一些基础知识

自动出价问题

基于 DT 的自动出价

GAVE 整体框架介绍

GAVE概述

Score-based RTG

Action Explorations

Learnable Value Function

Optimization Algorithm

离线实验

Experiment Setup

整体性能（RQ1）

一致性分析（RQ2）

参数分析（RQ3）

消融研究（RQ4）

在线部署

相关工作

离线强化学习和Decision Transformer

在线广告平台的自动出价

结论