CA——拍卖机制设计概述

注：论文主要参考自万字长文，漫谈广告技术中的拍卖机制设计（经典篇）等资料，有一些自己的思考

名词解释

  • 竞拍者 ：需求方，在广告系统中就是广告主
  • 机制拍卖中的一般假设 ：一般假设竞拍者是理性的，即满足个体理性（收益非负），且有能力通过调整自己的策略来获得更高的收益，
  • 私有信息（Private Value） ：也称为私有估值 ，竞拍者对物品、广告位的估值一般是私有信息，一些论文也称为Type类型 ，该信息是外部不可知的
    • 一些机制设计的目标就是诱导竞拍者在博弈中真实表达自己的私有信息（所以要设计他们说真话是他们的最优策略的机制）
  • 拍卖机制 ：包含分配规则（Allocation Rule）和计费规则（Payment Rule）两个部分
  • 效用（Utility） ：一般是价值减去支出即 效用函数 = 广告主获得的价值 - 广告主的支付价格，即 \(u = v - p\)
  • 广告主偏好 ：通常包含效用最大化（Utility Maximizer）和价值最大化（Value Maximizer）两种类型
  • 社会福利（Social Welfare） ：指的是整体广告主的价值和，单个广告主对单个广告位置的价值 = 广告主获得广告位的概率 * 广告位对广告主的价值
    • \(n\) 个竞拍者的社会福利可表示为 \(SW = \sum_{i=1}^n v_i x_i\)，其中 \(x_i\) 是竞拍者 \(i\) 获得物品的分配概率，\(v_i\) 是竞拍者 \(i\) 对该物品的估值
    • 社会福利的另一个视角：广告主效用为0时（即商家说真话且按照一价计费时），社会福利等于买家从广告主手里获得的收入 ，所以社会福利也可以表达为 在满足 IR 的情况下，社会福利等于买家可以从广告主手里获得的最大收入
  • 流动性福利（Liquid welfare）【未找到精确定义，待补充】 ：流动性福利是指存在预算约束情况下的社会福利（目前看到的都是预算约束下的流动性社会福利定义），表示在不违反财务约束的情况下可以从竞拍者中提取的最大收入 ，Auto-bidding and Auctions in Online Advertising: A Survey, 202408, Google 中有相关的定义（Truthful Auctions for Automated Bidding in Online Advertising, IJCAI 2023, Alibaba 中有ROI约束+预算约束下的定义）
    • \(n\) 个竞拍者的流动性福利可表示为\(\text{LW}=\sum_{i\in[n],u_{i}(t_{i},\mathbf{t}^{\prime})\geq 0}\min\left(\frac{v_{i }(\mathbf{t}^{\prime})}{R_{i}},B_{i}\right)\)，其中 \(R_i,B_i,v_i(\mathbf{t}^{\prime})\) 分别表示广告主设置的ROI，预算和广告主的累计价值 ，关于社会福利和流动性福利的更多讨论见附录
  • 有效机制（efficient mechanism） ：社会福利最大化的机制是对资源最有效率的配置方式，所以该类型的机制也叫有效机制
  • 最优机制（optimal mechanism） ：平台收入最大化的机制称为最优机制
  • 拍卖机制的目标 ：使得广告主竞价博弈收敛结果符合平台预期（平台预期包括平台收益、社会福利等）
    • 常见的目标包括社会福利最大化和平台营收最大化
  • 激励相容（Incentive Compatibility） ： 鼓励竞拍者讲真话
  • 优势策略激励相容（Dominant-Strategy Incentive Compatibility，简称DSIC） ：不管其他智能体如何报告自己的私有信息，如实报告（即讲真话）都是每个广告主的最优决策，即说真话时广告主效用最大化（效用最大化类型的用户）；
  • 贝叶斯纳什激励相容（Bayes-Nash Incentive Compatibility，简称BIC） ：如果其他广告主是如实报告自己的私有信息的，那么广告主最优反应也是如实报告
  • 完全信息设定 ：参与者知道其他参与方的真实类型
  • 不完全信息设定 ：参与者只知道其他参与方的类型分布（而不是真实类型）
  • 博弈均衡 ：博弈均衡是博弈论中的一个核心概念，它描述了在给定的博弈规则下 ，参与者选择某种策略后所达到的一种均衡状态（稳定状态）。在这种状态下 ，每个参与者都无法通过单方面改变自己的策略来获得更好的结果。换句话说，博弈均衡是一种策略组合 ，使得任何一个参与者都没有动机去单方面改变自己的策略
    • 纳什均衡 Nash Equilibrium（NE） ：在完全信息设定下的，一种在给定其他参与者策略时，任何单个参与者都没有动机去改变自己的策略的均衡状态
      • 囚徒困境是一个典型的纳什均衡，两者都选择说真话就是囚徒困境的纳什均衡状态
    • 贝叶斯纳什均衡 Bayesian Nash Equilibrium（BNE） ：一种在不完全信息设定下得，一种在给定其他参与者策略和类型分布（注意：只知道类型分布，不知道真实类型）时，没有参与者有动机单独改变其策略的均衡状态
      • 贝叶斯纳什均衡可以看做是对纳什均衡的一个扩展，用于处理不完全信息的情况
    • 优势策略均衡 Dominant Strategy Equilibrium（DSE） ：一种在完全信息或不完全信息设定下得，无论其他参与者选择什么策略 ，每个参与者策略总有自己的最优策略的均衡状态
      • 如果存在优势策略均衡，则它一定是唯一的纳什均衡 ，因为每个参与者都有明确的最佳行动，不受其他参与者行为的影响
      • 优势策略均衡一定是一个纳什均衡
    • 注：一个好的机制下，博弈结果可以有一个均衡 ，也可以有多个均衡 ，但不能是非均衡的
  • 直接显示机制（direct-revelation mechanism） ：要求参与者直接如实报告自己的私有信息（例如在拍卖中直接出价，而非通过复杂的行为间接传递信息）
    • 直接显示机制不一定满足 DSIC ：实际上，参与者会报告一个自己的类型空间中的值（不一定是真实的），即
    • 直接显示机制不一定存在均衡状态 ：可能竞拍者会来回调整他的报价，尝试拿到更优的收益
    • 注意：在一些书籍或博客中，会表达直接显示机制要求竞拍者如实报价 ，这会让人误以为直接显示机制都是 DSIC 的，我的理解是这并不代表机制是 DSIC 的，要求只是表达一个期望，要求了竞价者也不一定会如实上报
  • 可实施的分配规则 ：对于一个分配规则x ，如果存在一个扣费规则p ，使得直接显示机制 (x, p) 是满足 DISC 性质的，那么就称这个分配规则x是可实施的；

理想的拍卖机制是怎样的？

  • 高效率保证 ：多项式时间（一般近似线性）内完成分配和扣费两个计算过程
    • 为了可以应用，这个规则一般不可以做松弛
  • 高效果保证 ：存在均衡 ，且均衡结果满足引导预期 ，社会福利最大化或平台营收最大化；
    • 为了保证高效率保证 ，这个要求可以被松弛，主要是涉及到分配规则

      from 万字长文，漫谈广告技术中的拍卖机制设计（经典篇）
      因为最优分配问题本质是一个背包问题，而背包问题是NP困难问题，分配规则不可能在多项式时间内被实现，所以往往采用启发式的贪心算法，也就是业界常用的排序策略。这样分配问题就转化为了排序问题，例如论文开头Rankscore计算公式的设计，可以获得高效率的近似最优解

  • 高动机保证 ：优势策略激励相容（DSIC） ，即如实报价是参与者的优势策略（注意此时均衡不仅存在，而且是以最严格的优势策略均衡（DSE）的形式存在）；
    • 为了保证高效率保证 ，这个要求也可以被松弛，主要涉及到扣费规则

      from 万字长文，漫谈广告技术中的拍卖机制设计（经典篇）

      • Myerson引理证明当分配规则确定 ，扣费规则就是唯一的、且有明确的表达式 ，假设该表达式是a。可是实际环境非常复杂，或因为计算效率问题，或因为业务约束问题，导致实际采用的扣费规则没有用a，却用了b，那么DSIC就会被破坏
      • 但是非DSIC机制就一定很糟糕吗？答案非也。前文提到，优势策略均衡是最理想的均衡结果 ，机制设计的底限是要有均衡的预期 ，有均衡预期就有足够假设来预测智能体的行为，那么机制结果就能有效推演。所以非DSIC机制也可以有不错的均衡性质 ，它们在实际中很常见
      • 例如广告拍卖机制中，假设广告主偏好模式是Utility Maximizer ，平台优化目标是社会福利最大化 ，那么只有VCG机制满足 DSIC ，GSP机制不满足 DSIC ，但是也不妨碍GSP机制盛行，详细内容下文会重点介绍
  • 个人理解：
    • 拍卖机制能最大化社会福利的前提是竞拍者真实报告自己的类型，否则无法实现，故而要尽量保证 DSIC 才能尽量做到 社会福利最大化

Myerson 引理

  • 分配规则 ：一个分配规则是可实施 ，当且仅当它是单调的；
  • 扣费规则 ：如果分配规则是单调的，那么存在唯一的扣费规则 ，使得直接显示机制是 DSIC 的，且这个扣费规则有明确的表达式

拍卖形式的分类

  • 单物品拍卖和多物品拍卖 ：按拍卖品数量划分，有些文章也称为单位置拍卖和多位置拍卖
  • 单参数拍卖和多参数拍卖 ：按照竞拍者报价数量划分，注意是一次拍卖中，上报多个估值还是上报一个估值划分
  • 单轮拍卖和多轮拍卖 ：按照竞拍论述划分

    from 万字长文，漫谈广告技术中的拍卖机制设计（经典篇）
    轮数越多，竞拍者的私有信息Type会越来越成为公有信息，使得竞拍者能有更多的信息做决策从而调整报价策略。虽然多轮拍卖更加契合实际广告拍卖场景，广告主一笔预算往往会参与很多轮的请求报价，但是多轮的机制设计比单轮复杂很多，一般简化为单轮拍卖形式进行分析讨论

  • 无约束拍卖和有约束拍卖 ：按照竞拍者目标是否带着约束划分

    from 万字长文，漫谈广告技术中的拍卖机制设计（经典篇）
    有约束是指在广告主追求营销目标最大化的同时会带有指标约束，例如预算约束或者ROI约束等，这样广告主报价策略会从短期收益最大化调整为长期收益最大化，这对机制性质也会带来不小挑战

  • 注意：一般的广告拍卖场景中（包括万字长文，漫谈广告技术中的拍卖机制设计（经典篇）），一般都将广告的经典机制设计范畴规约在“异质多物品、单参数、单轮和无约束”拍卖形式下（简称多物品拍卖）

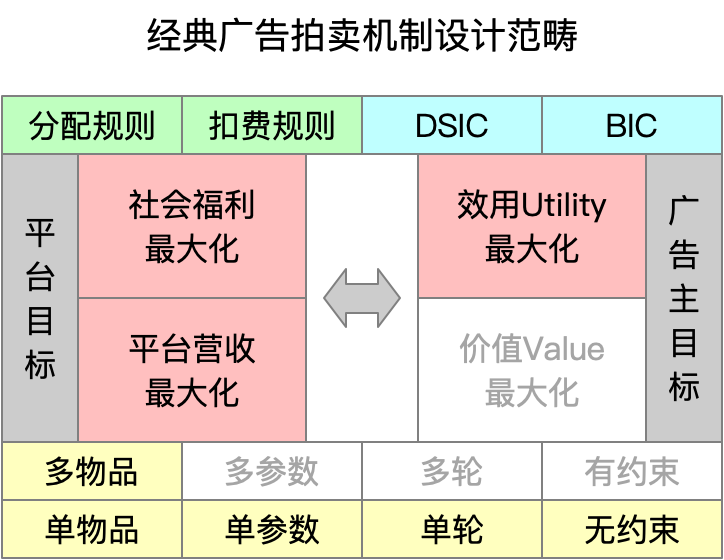
社会福利最大化的拍卖机制

  • 社会福利最大化的机制是对资源最有效率的配置方式，所以该类型的机制也叫有效机制（efficient mechanism）

SW最大化-单物品拍卖的有效机制

  • 二价计费（Second-price auction，简称SP）机制，也叫 Vickrey auction，是社会福利最大化的 DSIC 机制

SW最大化-多物品拍卖下VCG和GSP机制比较

VCG机制

  • 多物品拍卖下，若想要实现社会福利最大化 ，分配规则应该按照报价从高到低排序，第 \(i\) 高报价的竞拍者获得第 \(i\) 好的物品，此时，通过Myerson引理可以证明，满足DSIC的唯一支付公式是VCG扣费方式：
    $$ p_i = \sum_{j=i}^k b_{j+1} \frac{\alpha_j - \alpha_{j+1}}{\alpha_i} $$

    • 付费是该竞拍者赢得广告位后，给其他广告主带来的收益损失是该竞拍者需要支付的费用；直观理解为：从自己获得的这一物品起，后续所有物品上对其他人造成的损失和（因为后面每个竞拍者都因为竞拍者 \(i\) 的存在而后移一位，所以可以如上式表示社会福利），一般的论文中，也常常也表示为：
      $$ p_i = SW_{-i} - (SW - v_i x_i) $$
      • \(SW_{-i}\) 是竞拍者 \(i\) 不参与竞拍时的其他人获得的总社会福利
      • \(SW - v_i x_i\) 是竞拍者 \(i\) 参与竞拍时的其他人获得的总社会福利 ， \(SW\) 则表示包括竞拍者 \(i\) 在内的总体社会福利

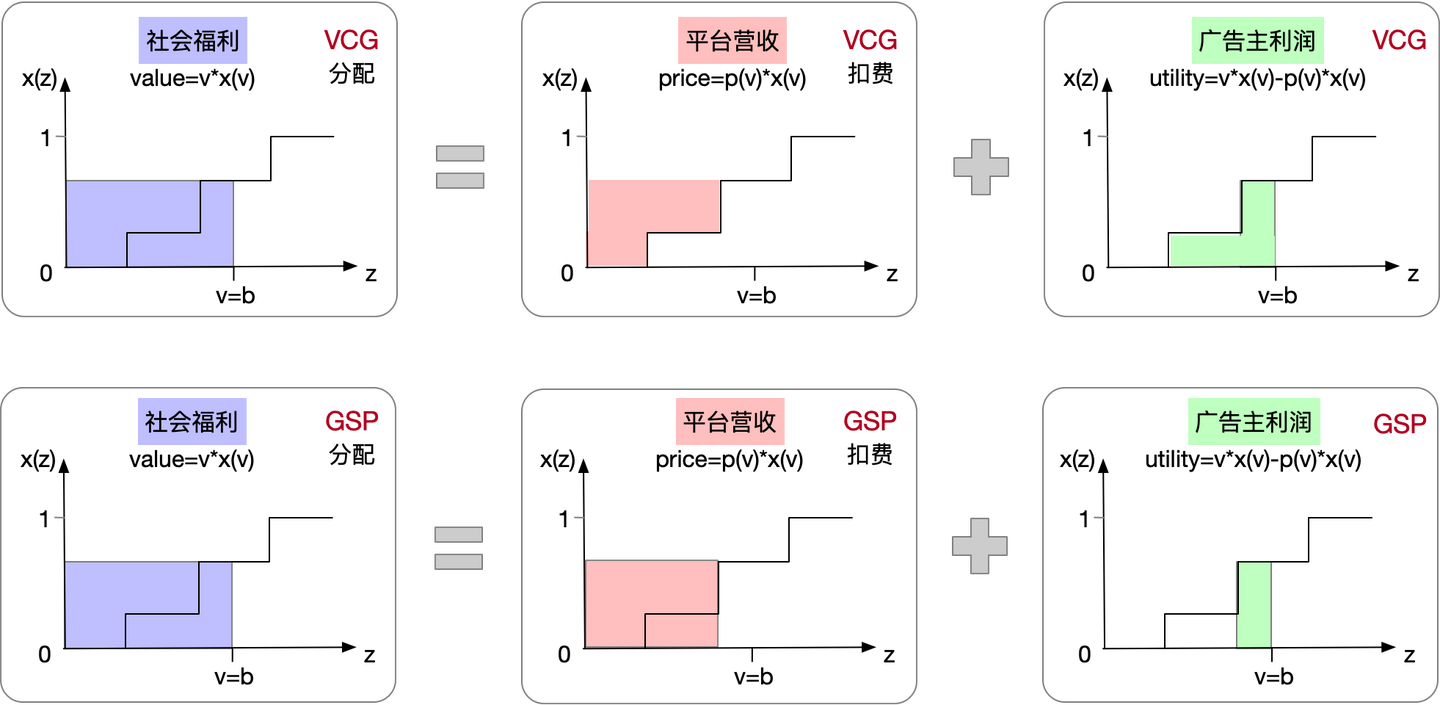
  • 多物品拍卖下的Vickrey–Clarke–Groves auction（简称VCG机制）是单物品拍卖下的Vickrey auction（也称SP机制）有效升级，下图准确表示了 VCG 机制是满足 DSIC 的：

    • \(z\) 表示估值分布，\(v\) 表示真实估值，\(b\) 表示报价；\(x(z)\) 表示分配结果（对应为点击率），\(p(v)\) 或 \(p(b)\) 表示计费结果
    • 三列分别为出真实价值 \(b = v\)，出高价 \(b > v\) 和出低价 \(b < v\) 的情况
    • 第一行表示不同出价 \(b\) 下获得的价值，第二行表示支付金额，第三行表示效用(Utility) = 价值 - 支付，即 \(u = v\cdot x(b) - p(b)\)
    • 阶梯函数是因为在不同的位置，点击率不同，但同一个位置，随着出价变化，点击率是相同的
    • 图中绿色部分就是收益部分（注：第三行第二列中绿色区间还要减去阴影部分才可以），显然说真话是效用是最大的

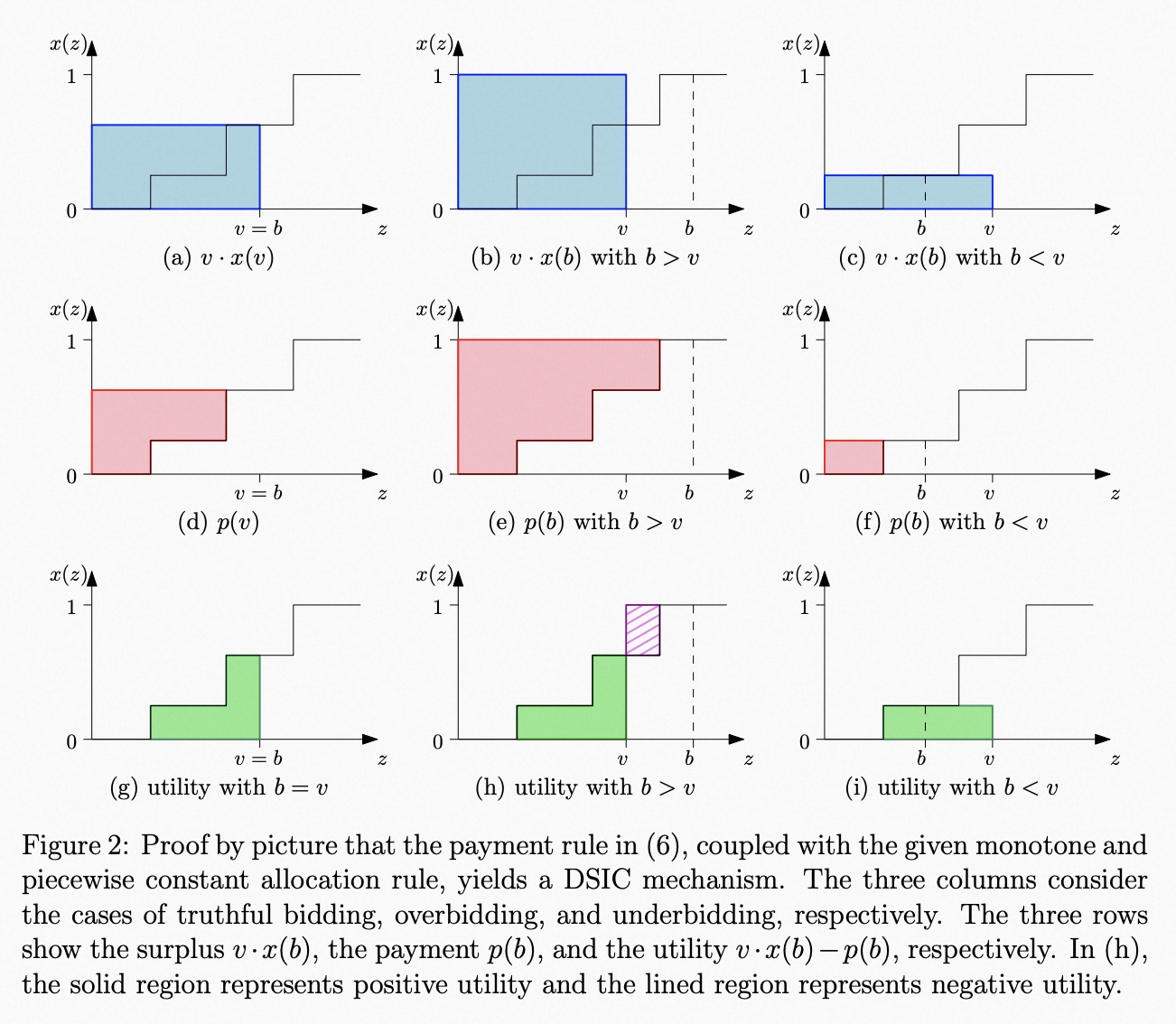
  • 多物品拍卖下，若目标是社会福利最大化 ，则VCG机制是满足 DSIC 机制的唯一机制

    • 单物品拍卖下，若目标是社会福利最大化 ，SP机制是满足 DSIC 机制的唯一机制
    • 单物品拍卖下，若目标是平台收入最大化 ，Myerson拍卖机制是满足 DSIC 机制的机制（并非唯一？）

  • VCG机制的缺点 ：

    • 计算复杂 ：运行效率低下，运算复杂（比如一些场景中需要做listwise的CTR预估）
    • 平台收入低 ：平台收入较低（比GSP等都低，可以认为是常见的收入最低的拍卖形式，唯一的优点是满足 DSIC）
    • 解释成本高 ：给广告主解释困难

GSP机制

  • GSP机制（Generalized second-price auction）分配规则和VCG一样，按照下一位出价计费：
    $$ p_i = b_{i+1} $$
  • 类似上面 VCG 机制的分析图，下图展示了 GSP 机制的分析情况：
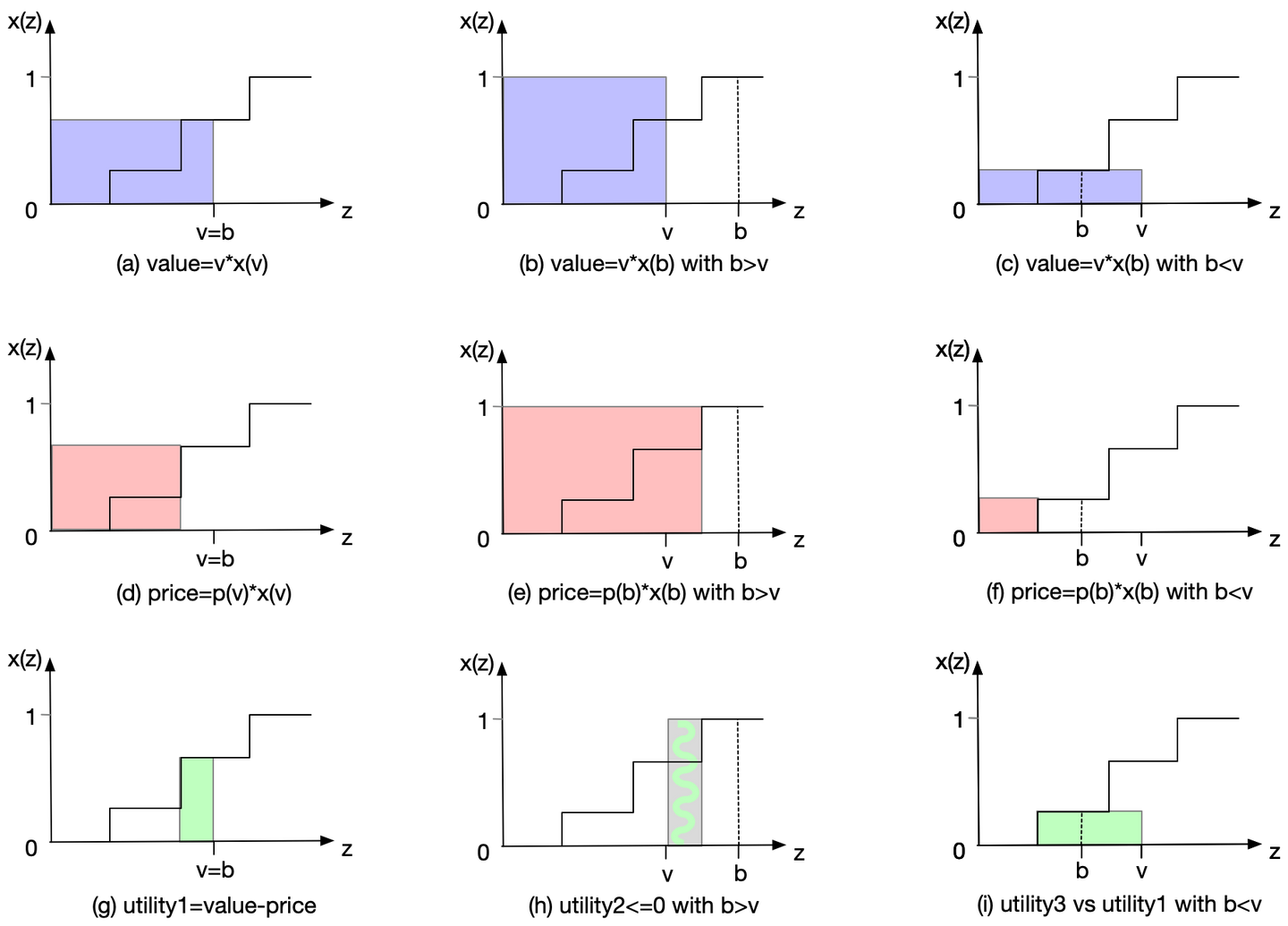
    • 可以看到，报高价没有正向收益（第三行第二列），但是报低价有可能获得更高的效用（第三行第三列和第三行第一列的绿色区域孰高孰低不一定）
  • 广告主是效用最大化类型时，GSP虽然不是 DSIC 的，但是其有不错的均衡性质（机制要求均衡且均衡状态满足机制目标即可，不一定要 DSIC ，DSIC 是个非常强的性质），GSP包含两个视角的均衡 ：
    • Pure Nash Equilibrium under Full-Information Setting ：完全信息设定下的纳什均衡？
    • Bayesian Nash Equilibrium under Partial-Information Setting ：不完全信息设定下的贝叶斯纳什均衡？

      from 万字长文，漫谈广告技术中的拍卖机制设计（经典篇）
      以前者（理解：这里指Pure Nash Equilibrium under Full-Information Setting）为例，假设多轮竞价交互之后广告主的估值成为公有信息，GSP机制达到的一种均衡结果是广告主会认为保留当前位置是最优策略，不愿意与比他顺位高的人换位置，不然利润受损，这种均衡叫 locally envy-free equilibrium（也称symmetric Nash equilibrium），对应广告主的报价策略不再是如实报价，详细可见文献

  • GSP优点缺点总结 ：
    • 计算简单 ：仅需一个简单公式，容易落地
    • 平台收入高 ：收入更高，对照VCG和GSP的分析图中第二行可得
    • 容易解释 ：按照下一位出价计费，简单易懂
    • DSIC讨论 ：在广告主是效用最大化类型时，GSP不是 DSIC的（有文献提到，在广告主是Value最大化类型时，GSP机制是 DSIC 的）
    • 均衡性讨论 ：GSP存在多个均衡，GSP的其中一个均衡结果和VCG等价（注：此时因为扣费大于VCG，所以平台营收会比VCG更高）
      • 问题：这里的与VCG等价是说，在这个均衡状态下，大家都会说真话吗？存在部分竞拍者会试探低价吧？

SW最大化-GSP机制关于点击率的升级

  • 下面的内容主要考虑关于点击广告（按点击售卖的广告）场景，目标还是如何优化社会福利，更好的实现社会福利最大化，提高资源分配效率

GSP

  • 普通的GSP认为点击率只与广告位置有关，与广告主无关，未考虑不同竞拍者（广告实体）的点击率在同一个位置会不同
  • 下文中也称广告自身的点击率为广告质量分

wGSP

  • wGSP（weighted GSP）引入一个与竞拍者 \(i\) 相关的点击率 \(\beta_i\)（也称为广告质量分）
    • 注：wGSP并没有假设广告在不同位置会有不同的广告质量分（理解：这里的质量分是与广告位置无关的，用户和广告之间的匹配分数）
  • 此时社会福利是（\(n\) 个广告主， \(k\) 个资源位）：
    $$ SW = \sum_{i=1}^n \sum_{j=1}^k v_i \beta_i \alpha_j $$
  • 广告主的效用是：\(u_i = \beta_i \alpha_j(v_i - p_i)\)，注：效用也是效用最大化类型广告主的优化目标
  • wGSP分配规则 ：按照 \(\beta b \) 排序
  • wGSP计费规则为：
    $$ p_i = \frac{\beta_{i+1} b_{i+1}}{\beta_i} $$

iGSP

  • wGSP没有考虑广告在不同位置会有不同的广告质量分（点击率），实际上，不同位置上、同一位置不同上下文情况下广告的点击率均会有不同
  • iGSP（iterated GSP）考虑了广告在不同位置会有不同的广告点击率，但仅仅可以在做到2个资源位同时拍卖的情况下，最大限度保证 existence of efficient equilibria ，3个资源位的情况还没解决
    • 问题：如何理解最大限度保证 existence of efficient equilibria？
  • iGSP分配规则 ：逐个位置拍卖，逐个位置预估考虑到上下文、位置因素下的每个广告主的点击率 \(\gamma_{ij}\)，然后按照价高者得
  • iGSP计费规则 ：每次拍卖时，对当前拍卖位置的首位广告主（当前位置竞胜者）进行二价计费：
    $$p_{1j} = \frac{\gamma_{2j}b_2}{\gamma_{1j}}$$
  • 竞胜后的广告主不参与下一轮位置竞争，遍历拍卖至资源分配完
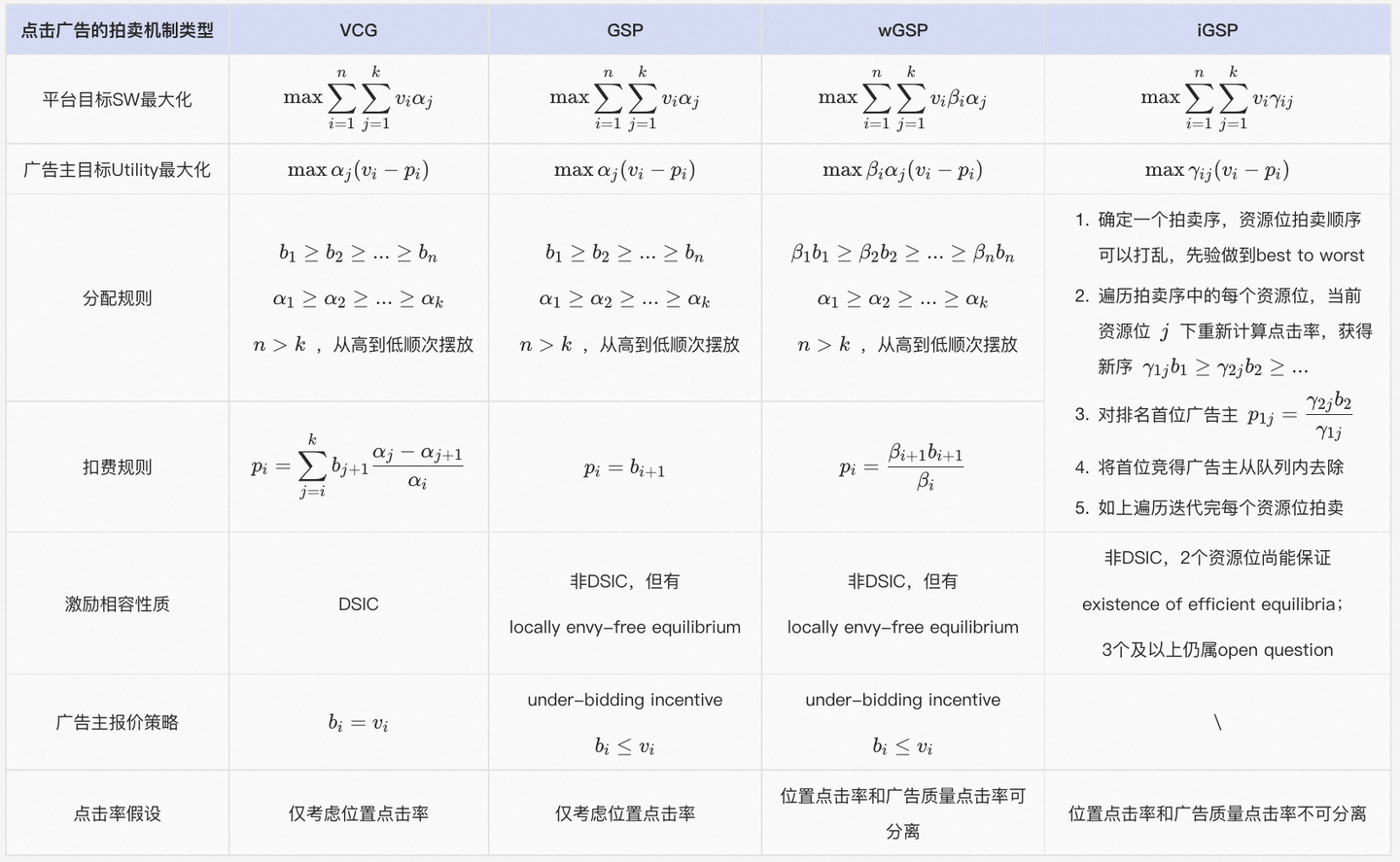
  • iGSP的总结：相对于wGSP，拍卖流程更复杂，但因为考虑到广告在不同位置下的质量分，会使得社会福利更优（资源配置效率更高）

平台收入最大化的拍卖机制

  • 满足 DSIC 性质，且使得平台收入最大化（Revenue最大化，简称Rev最大化）的机制称为 最优机制（optimal mechanism）

Rev最大化-VCG与GSP的平台收入比较

  • GSP的收入更高，对平台来说，GSP机制更受欢迎
  • GSP机制不再是 DSIC 的（从前文看，广告主有隐瞒估值，刻意报低价的动机），但GSP机制有均衡性质（注意：均衡结果是最起码的要求，否则从长期博弈结果来看短期的平台营收都不可持续）

    from 万字长文，漫谈广告技术中的拍卖机制设计（经典篇）
    换个角度解释这个现象，GSP机制不是DSIC的，广告主有隐瞒估值低报价的动机，所以长期来看会随着广告主低报价整体社会福利不如VCG，使得虽然在分蛋糕方面GSP有优势但在做大蛋糕方面存在不利因素，此消彼长，长期看平台营收GSP一定会打折扣。GSP有不错的均衡性质尚且如此，更何况其他粗暴魔改扣费规则的机制了，所以事情看来没有那么简单

Rev最大化-单物品拍卖的最优机制

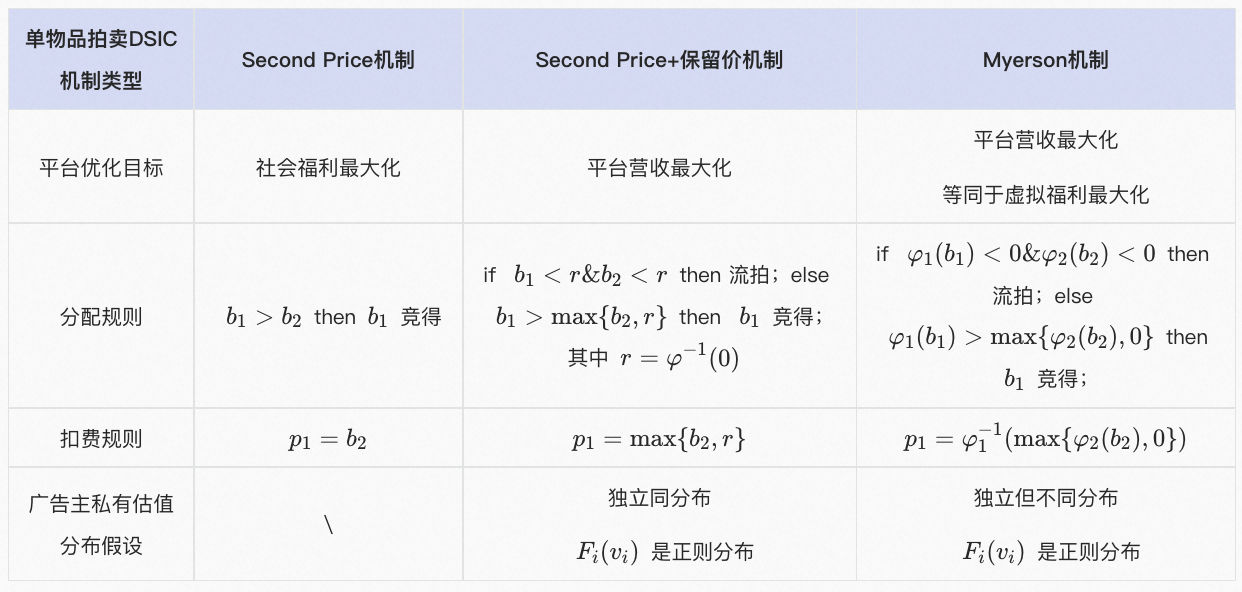
  • SP机制：Second Price，二价计费
  • SP+保留价机制：二价计费，同时带有保留价，当低于保留价时，不售卖，高于保留价时，保留价参与二价计算（即广告主计费不会低于保留价）
  • Myerson机制：可以获得最大化期望收益的最优机制
    • 注：在竞拍者私有估值服从独立同步分布时，Myerson拍卖机制等价于SP+保留价 \(\varphi_i^{-1}(0)\) 机制
  • 其他补充：

    from 万字长文，漫谈广告技术中的拍卖机制设计（经典篇）
    首先定义虚拟估值 \(\varphi_i(v_i) = v_i - \frac{1-F_i(v_i)}{f_i(v_i)}\)，它和私有估值 \(v_i\) 以及分布 \(F\) 有关；然后可以论证在满足DSIC的机制空间上对期望收益最大化 ，可以等同于在同一个空间对期望虚拟福利最大化 ，这样原本关心的收益最大化问题就转变为了分配最优化问题， \(Rev = \max\sum_{i=1}^n \varphi_i(v_i) x_i\)，与前文章节中 \(SW = \max\sum_{i=1}^n v_i x_i\) 相比仅仅是将私有估值 \(v_i\) 转换为对应的虚拟估值 \(\varphi_i(v_i)\)，其他分配规则的细节以及扣费规则都与社会福利最大化一模一样；最后只需要保证 \(\varphi_i(v_i)\) 是单调的，即私有估值的分布 \(F_i(v_i)\) 是正则分布 ，许多常见分布基本都是正则分布，例如normal、lognormal、uniform and exponential distributions等；非正则分布包括多峰分布和长尾分布，分配的单调性是机制DSIC性质的前提。论证过程可详见文献
    可以发现虚拟估值 \(\varphi_i(v_i)\) 可能为负，在分配的过程中如果遇到 \(\varphi_i(v_i) < 0\) 的竞拍者会被剥夺竞拍资格，如果所有竞拍者的虚拟估值均为负，则流拍，所以 \(\varphi_i^{-1}(0)\) 即虚拟估值为0的逆函数起到了个性化保留价的功能。如果假设所有竞拍者的私有估值服从独立但不同分布，则不仅会有各自不同的保留价，还会遇到如实报价情况下报价高，但虚拟估值不一定高，导致没有竞得更好的资源位，也好理解，此时虚拟估值代表了个性化自己和自己对比的报价意愿强烈程度；如果假设所有竞拍者的私有估值服从独立同分布，因为估值分布相同则虚拟估值函数 \(\varphi\) 也相同，又因为估值分布 \(F\) 服从正则分布，则 \(\varphi\) 严格递增，那么虚拟估值最高的竞拍者就是私有估值最高的竞拍者，这样虚拟福利最大化机制就和带有保留价 \(\varphi_i^{-1}(0)\) 的二价机制相同，回答上文提到的两个竞拍者估值服从独立同分布 \([0,1]\) 均匀分布的例子，\(\varphi_i^{-1}(0)=\frac{1}{2}\) S确实是最优保留价。以下是单物品拍卖的几个机制对比：

Rev最大化-多物品拍卖下GSP的改造

  • Myerson拍卖无法应对多物品拍卖位置，实际上，自1981年Myerson拍卖问世以来，至今没有找到多物品拍卖设定下的最优拍卖机制，多物品拍卖设定下的最优拍卖机制（满足 DSIC 的收益最大化拍卖）设计是一个开放性问题
  • 在多物品拍卖场景，广告多坑位拍卖一般围绕改造 GSP 机制来近似实现最优结果，具体来说，是将Myerson机制和GSP机制结合起来

mGSP

  • mGSP（myerson GSP）机制，将Myerson保留价技术直接应用到wGSP机制上

    from 万字长文，漫谈广告技术中的拍卖机制设计（经典篇）
    和单物品拍卖的设计思路类似，Myerson保留价最核心的虚拟估值依赖广告主的私有估值分布，系统可以酌情根据独立同分布的颗粒度进行假设的调整，例如客户之间完全独立不同分布、相同搜索词的客户之间独立同分布、整体流量客户独立同分布等。因为广告系统是多轮拍卖系统，假设广告主是如实报价，则私有估值分布可以根据广告主历史报价进行不同粒度的分布拟合，从而得到虚拟估值。有了虚拟估值和保留价，在分配规则方面有两种类型可做尝试：Eager模式，先过滤后排序，即先根据保留价过滤没有竞争力的广告主，再按照虚拟估值排序；Lazy模式，先排序后过滤。Eager模式对最高报价无法胜出保留价的情形更友好，Lazy模式对第2高报价无法胜出保留价的情形更友好，多数情况下Eager模式在提营收方面会比Lazy更有优势

aGSP

  • aGSP（anchoring GSP）机制，是对mGSP机制一种松弛方式

    from 万字长文，漫谈广告技术中的拍卖机制设计（经典篇）
    第二种是aGSP（anchoring GSP）机制，是对mGSP机制一种松弛方式，业务落地过程中虚拟估值的求逆计算和私有估值的正则分布要求等均会让机制实现不够简洁且解释性较差，略牺牲效果的情况下精简机制设计也是可接受的迭代方向。首先保留价的计算方法和mGSP机制相同，一般保留价的颗粒度会选择数据积累较为充分的粒度。其次主要差异点就是将虚拟估值由 \(\varphi_i(v_i) = v_i - \frac{1-F_i(v_i)}{f_i(v_i)}\) 简化为 \(\varphi_i(v_i) = v_i - r_i\)，如果假设私有估值分布是均匀分布，化简的表达式就非常接近，求逆也方便，而且业务含义与myerson思路很吻合，报价竞争力更多看重每个广告主超出个性化保留价的那部分

rGSP

  • rGSP（reserve GSP）机制，是对aGSP机制更加进一步的松弛

    from 万字长文，漫谈广告技术中的拍卖机制设计（经典篇）
    因为有文献提出，为了解决私有估值和虚拟估值趋势不一致问题，虚拟估值可以仅用于个性化保留价的过滤，分配和扣费依然按照私有估值进行，这样虽然对营收有折损但是机制实现更加简洁且易解释

一些讨论

  • 机制设计应该关注用户体验 ：相对免费资源位置，付费资源位置本质是在牺牲用户体验，换取社会福利和平台收入，机制设计时还需要考虑用户体验，否则如果用户失去对付费资源的关注度，则平台将彻底失去流量变现机会
  • 未来方向：
    • 广告主偏好：论文主要是以效用Utility最大化为目标，后续可考虑以价值Value最大化为目标的情况
    • 结合自动出价（Auto-Bidding）：自动出价的场景越来越多，但相关的机制研究较少
    • 基于学习的机制（数据驱动）
    • 生成式拍卖

附录：社会福利和流动性福利的讨论

  • 社会福利（Social Welfare） ：指的是整体广告主的价值和，单个广告主对单个广告位置的价值 = 广告主获得广告位的概率 * 广告位对广告主的价值
    • \(n\) 个竞拍者的社会福利可表示为
      $$SW = \sum_{i=1}^n v_i x_i$$
      • 其中 \(x_i\) 是竞拍者 \(i\) 获得物品的分配概率，\(v_i\) 是竞拍者 \(i\) 对该物品的估值
    • 社会福利的另一个视角：广告主效用为0时（即商家说真话且按照一价计费时），社会福利等于买家从广告主手里获得的收入 ，所以社会福利也可以表达为 在满足 IR 的情况下，社会福利等于买家可以从广告主手里获得的最大收入
      • 对最大的理解 ：这里最大是指刚好满足 IR，即商家效用为0时的值，是社会福利定义里面针对约束而言的“最大”，拍卖机制中常说的社会福利最大化的“最大”是分配效率
      • 机制拍卖的目标 ：这个视角同时暗示了，平台收入小于等于社会福利 ，平时我们拍卖机制设计中，最大化社会，一方面在提升资源分配率 ，另一方面也等价于是在提升平台收入空间（因为在IR约束下，平台收入不会超过社会福利）
  • 流动性福利（Liquid welfare）【未找到精确定义，待补充】 ：流动性福利是指存在预算约束情况下的社会福利（目前看到的都是预算约束下的流动性社会福利定义），表示在不违反财务约束的情况下可以从竞拍者中提取的最大收入 ，Auto-bidding and Auctions in Online Advertising: A Survey, 202408, Google 中有相关的定义（Truthful Auctions for Automated Bidding in Online Advertising, IJCAI 2023, Alibaba 中有ROI约束+预算约束下的定义）
    • \(n\) 个竞拍者的流动性福利可表示为
      $$\text{LW}=\sum_{i\in[n],u_{i}(t_{i},\mathbf{t}^{\prime})\geq 0}\min\left(\color{red}{\frac{v_{i }(\mathbf{t}^{\prime})}{R_{i}}},B_{i}\right)$$
      • 其中 \(R_i,B_i,v_i(\mathbf{t}^{\prime})\) 分别表示广告主设置的ROI，预算和广告主的累计价值
      • 注意，其实 \(\color{red}{\frac{v_{i }(\mathbf{t}^{\prime})}{R_{i}}}\) 就是ROI出价下的社会福利，为了方便理解，可以推导出价点在ROI上的商家的曝光 \(j\) 上的私有价值等于 \(CTR_{ij} \times CVR_{ij} \times Price_{ij} \times \frac{1}{ROI}\)，而广告主 \(i\) 的累计收益为 \(\color{red}{v_i(\mathbf{t}^{\prime})} = \sum_j CTR_{ij} \times CVR_{ij} \times Price_{ij}\)
  • 流动性福利和社会福利的本质是一样的（可以理解为是同一个指标在不同场景下的不同定义），都是在满足一定约束条件下，买家可以从广告主手里获得的最大收入（这里的最大是针对约束而言的）
    • 社会福利 ：只有 IR 约束 ，这个 IR 约束主要针对出价，出价就是商家的私有价值，可以是 ROI 约束 或 CPA 约束
    • 流动性福利 ：除了 IR 约束，还有预算约束
    • 在预算约束无限时（或不生效时） ，社会福利等价于流动性福利 ，此时有:
      $$SW = LW = \sum_{i\in[n],u_{i}(t_{i},\mathbf{t}^{\prime})\geq 0} \color{red}{\frac{v_i(\mathbf{t}^{\prime})}{R_i}}$$