CA——各种拍卖机制总结

参考链接：
- 万字长文，漫谈广告技术中的拍卖机制设计（经典篇）

Myerson拍卖

Myerson机制就是单物品拍卖下，可以获得最大化期望收益的最优机制

from 万字长文，漫谈广告技术中的拍卖机制设计（经典篇）
Myerson机制就是可以获得最大化期望收益的最优机制。首先定义虚拟估值 $\varphi_i(v_i) = v_i - \frac{1-F_i(v_i)}{f_i(v_i)}$，它和私有估值以及分布有关；然后可以论证在满足DSIC的机制空间上对期望收益最大化 ，可以等同于在同一个空间对期望虚拟福利最大化 ，这样原本关心的收益最大化问题就转变为了分配最优化问题， $Rev = \max\sum_{i=1}^n \varphi_i(v_i) x_i$，与前文2.1.章节中 $SW = \max\sum_{i=1}^n v_i x_i$ 相比仅仅是将私有估值 $v_i$ 转换为对应的虚拟估值 $\varphi_i(v_i)$，其他分配规则的细节以及扣费规则都与社会福利最大化一模一样；最后只需要保证 $\varphi_i(v_i)$ 是单调的，即私有估值的分布 $F_i(v_i)$ 是正则分布 ，许多常见分布基本都是正则分布，例如normal、lognormal、uniform and exponential distributions等；非正则分布包括多峰分布和长尾分布，分配的单调性是机制DSIC性质的前提。论证过程可详见文献
可以发现虚拟估值 $\varphi_i(v_i)$ 可能为负，在分配的过程中如果遇到 $\varphi_i(v_i) < 0$ 的竞拍者会被剥夺竞拍资格，如果所有竞拍者的虚拟估值均为负，则流拍，所以 $\varphi_i^{-1}(0)$ 即虚拟估值为0的逆函数起到了个性化保留价的功能。如果假设所有竞拍者的私有估值服从独立但不同分布，则不仅会有各自不同的保留价，还会遇到如实报价情况下报价高，但虚拟估值不一定高，导致没有竞得更好的资源位，也好理解，此时虚拟估值代表了个性化自己和自己对比的报价意愿强烈程度；如果假设所有竞拍者的私有估值服从独立同分布，因为估值分布相同则虚拟估值函数 $\varphi$ 也相同，又因为估值分布 $F$ 服从正则分布，则 $\varphi$ 严格递增，那么虚拟估值最高的竞拍者就是私有估值最高的竞拍者，这样虚拟福利最大化机制就和带有保留价 $\varphi_i^{-1}(0)$ 的二价机制相同，回答上文提到的两个竞拍者估值服从独立同分布 $[0,1]$ 均匀分布的例子，$\varphi_i^{-1}(0)=\frac{1}{2}$ S确实是最优保留价。以下是单物品拍卖的几个机制对比：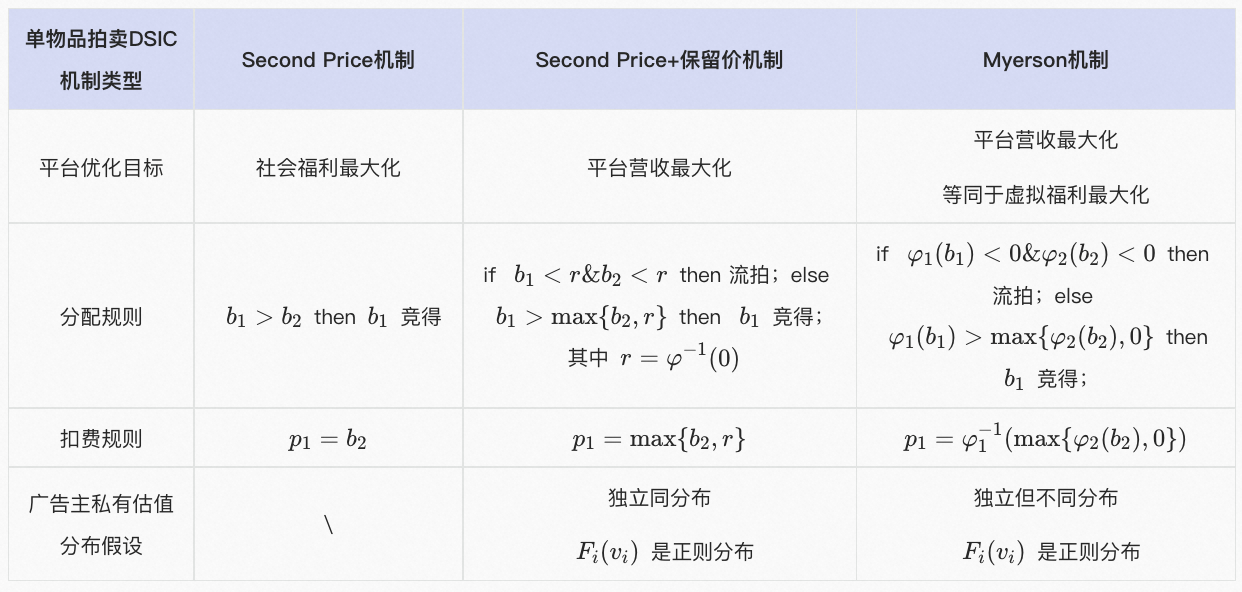

VCG

Vickrey-Clarke-Groves (VCG)

普通的VCG

WVCG

Weighted Vickrey-Clarke-Groves (WVCG)，带权重的VCG机制，是对原始VCG的改进，收入高于VCG机制

VVCA

SW-VCG

SW-VCG, Score-Weighted VCG
原始论文：Learning-Based Ad Auction Design with Externalities: The Framework and A Matching-Based Approach
博客：KDD’23 | Score-Weighted VCG：考虑外部性的智能拍卖机制设计

GSP

一些对比 from 万字长文，漫谈广告技术中的拍卖机制设计（经典篇）：

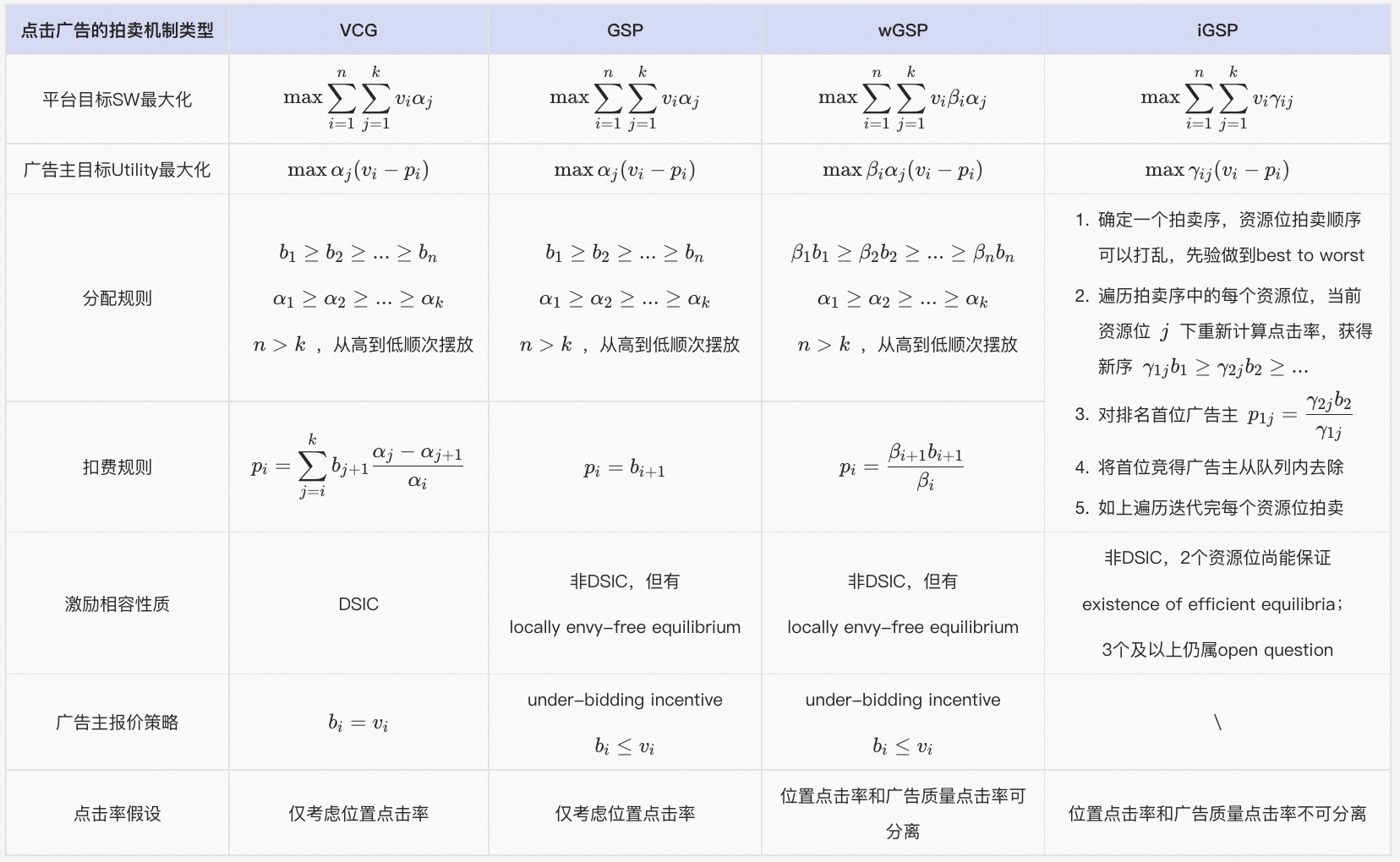
普通的GSP

uGSP

Utility-based Generalized Second Price auction (uGSP)，最早提出于论文 Optimising trade-offs among stakeholders in ad auctions, Microsoft Research, 2014. 是对GSP的一种扩展，其分配规则中的排序公式为：
$$ r_i(b_i) = \lambda_1 \times b_i \times pCTR_i + o_i $$
- 其中 $o_i$ 表示其他效用指标，比如作者使用了 $o_i = \lambda_2 \times pCTR_i + \lambda_3 \times pCVR_i$
支付规则与GSP相同，都是通过下一位的排序分反算计费

wGSP

wGSP（weighted GSP，weighted体现在广告质量分的引入），排序时会在出价上乘以这个权重 $\beta \cdot bid$ 来排序

mGSP

mGSP（myerson GSP）机制，将Myerson保留价技术直接应用到wGSP机制上

from 万字长文，漫谈广告技术中的拍卖机制设计（经典篇）
和单物品拍卖的设计思路类似，Myerson保留价最核心的虚拟估值依赖广告主的私有估值分布，系统可以酌情根据独立同分布的颗粒度进行假设的调整，例如客户之间完全独立不同分布、相同搜索词的客户之间独立同分布、整体流量客户独立同分布等。因为广告系统是多轮拍卖系统，假设广告主是如实报价，则私有估值分布可以根据广告主历史报价进行不同粒度的分布拟合，从而得到虚拟估值。有了虚拟估值和保留价，在分配规则方面有两种类型可做尝试：Eager模式，先过滤后排序，即先根据保留价过滤没有竞争力的广告主，再按照虚拟估值排序；Lazy模式，先排序后过滤。Eager模式对最高报价无法胜出保留价的情形更友好，Lazy模式对第2高报价无法胜出保留价的情形更友好，多数情况下Eager模式在提营收方面会比Lazy更有优势

aGSP

aGSP（anchoring GSP）机制，是对mGSP机制一种松弛方式

from 万字长文，漫谈广告技术中的拍卖机制设计（经典篇）
第二种是aGSP（anchoring GSP）机制，是对mGSP机制一种松弛方式，业务落地过程中虚拟估值的求逆计算和私有估值的正则分布要求等均会让机制实现不够简洁且解释性较差，略牺牲效果的情况下精简机制设计也是可接受的迭代方向。首先保留价的计算方法和mGSP机制相同，一般保留价的颗粒度会选择数据积累较为充分的粒度。其次主要差异点就是将虚拟估值由 $\varphi_i(v_i) = v_i - \frac{1-F_i(v_i)}{f_i(v_i)}$ 简化为 $\varphi_i(v_i) = v_i - r_i$，如果假设私有估值分布是均匀分布，化简的表达式就非常接近，求逆也方便，而且业务含义与myerson思路很吻合，报价竞争力更多看重每个广告主超出个性化保留价的那部分

rGSP

rGSP（reserve GSP）机制，是对aGSP机制更加进一步的松弛

from 万字长文，漫谈广告技术中的拍卖机制设计（经典篇）
因为有文献提出，为了解决私有估值和虚拟估值趋势不一致问题，虚拟估值可以仅用于个性化保留价的过滤，分配和扣费依然按照私有估值进行，这样虽然对营收有折损但是机制实现更加简洁且易解释

iGSP

iGSP（iterated GSP）可以最大限度保证 existence of efficient equilibria，但也仅限2个资源位同时拍卖，如果遇到3个及以上就仍然是一个 open question，不过还算乐观的情况是移动端的资源位往往较少

sGSP

原始论文：Revenue analysis of a family of ranking rules for keyword auctions
sGSP(squashing GSP)

from 万字长文，漫谈广告技术中的拍卖机制设计（经典篇）
另外一类不是在报价因子上做文章，而是在wGSP的广告质量点击率上做文章，通过对广告质量点击率进行挤压，也能达到提升营收的效果，这类机制叫做sGSP（squashing GSP）机制。分配规则是按照 $\beta^s_i b_i$ 进行排序，其中 $s$ 就是挤压因子，扣费规则按照 $p_i = \frac{\beta^s_{i+1} b_{i+1}}{\beta^s_i} = \left( \frac{\beta_{i+1}}{\beta_i} \right)^s b_{i+1}$。该挤压因子能够体现三方面的结论：1）Efficiency视角：当 $s=1$ 是社会福利最大化及Efficiency最大化，凡是 $s \neq 1$ 的调节都提升平台的短期收入，从而影响广告主价值；2）Relevance视角：只要 $s$ 往大调节，整体点击率就会提升，相关性就会变好；3）Revenue视角，当相邻广告质量随排序递减即 $\frac{\beta_{i+1}}{\beta_i} < 1$ ，在不改变排序的情况下调小 $s$，$p_i$变大，利好营收增加，当相邻广告质量随排序递增即 $\frac{\beta_{i+1}}{\beta_i} < 1$，在不改变排序的情况下调大 $s$，$p_i$变大，利好营收增加。这一方案为了进一步挖掘营收空间，可以升级为分位置调控挤压因子等，具体详见文献